$next$ $up$ $previous$ $contents$
Next: L'equazione di quarto grado Up: Le lezioni Previous: L'equazione di terzo grado Indice

Subsections

Casus Irreducibilis

La teoria

Da un esercizio di Jacobson, ma i dettagli sono quelli di [vdW71, § 64].

Sia $F \subseteq \mathbf{R}$ un campo, $f(x) = x^{3} + b x + c \in F[x]$ irriducibile, con tre radici reali che sono quindi (ovviamente distinte). Il discriminante è dunque positivo, in quanto è il quadrato di un numero reale. Il polinomio resta irriducibile in $F (\sqrt{D})$ , dato che altrimenti quest'ultima estensione, che ha al più grado due su , conterrebbe una radice di , che ha grado tre su . Possiamo quindi rimpiazzare con $F (\sqrt{D})$ , ovvero supporre che contenga $\sqrt{D}$ . Con questa ridefinizione, otteniamo che il campo di spezzamento ha grado su . Vogliamo far vedere che non esiste alcuna estensione radicale , con $E \subseteq M \subseteq \mathbf{R}$ . In altre parole, i numeri complessi non reali che compaiono nelle formule di Cardano sono inevitabili.

Esplicitamente

Teorema 1 Sia $F \subseteq \mathbf{R}$ un campo.

Sia $f(x) = x^{3} + b x + c \in F[x]$ un polinomio irriducibile, con tre radici reali. Sia il suo campo di spezzamento.

Allora non esiste alcuna estensione radicale tale che

$\displaystyle E \subseteq M \subseteq \mathbf{R}.$

Una semplice riduzione ci porta a considerare il caso in cui $M = F (\alpha)$ , con $\beta = \alpha^{p} \in F$ , per qualche numero primo $p \ge 3$ . Ora qualunque sia il campo (ma diciamo di caratteristica zero), vale il seguente semplice fatto

Lemma 2 Se il polinomio $g(x) = x^{p} - \beta \in F[x]$ è riducibile allora ha una radice in

, ovvero esiste $\gamma \in F$ tale che $\gamma^{p} = \beta$ .

Si può dire di più se il campo contiene le radici dell'unità (vedi [vdW71]): non sarebbe difficile completare la dimostrazione per vedere che allora si riduce completamente.

Dimostrazione. Sia $\alpha$ una fissata radice di

nel suo campo di spezzamento, sicché $\alpha^{p} = \beta$ . Nel suo campo di spezzamento,

si fattorizza dunque come

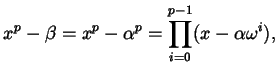$\displaystyle x^{p} - \beta = x^{p} - \alpha^{p} = \prod_{i=0}^{p-1} (x - \alpha \omega^{i}),$

ove $\omega$ è una radice primitiva

-sima di

. Supponiamo quindi che questo polinomio si fattorizzi propriamente in

come

$\displaystyle x^{p} - \beta = \varphi (x) \psi(x),$

con $\varphi , \psi \in F[x]$ , e $\grado(\varphi ) = \mu$ , con $0 < \mu < p$ . Allora (a meno di segni) il coefficiente costante di $\varphi$ , che è un certo $\delta \in F$ , è della forma $\delta = \alpha^{\mu} \omega^{s} \in F$ , e si ha $\delta^{p} = (\alpha^{\mu} \omega^{s}) = \beta^{\mu}$ . Dato che $\mu$ è coprimo con

, esistono

tali che $1 = \mu c + p d$ . Si ha

$\displaystyle \beta = \beta^{1} = \beta^{\mu c} \beta^{p d} = (\delta^{c} \beta^{d})^{p}.$

Basta ora prendere $\gamma = \delta^{c} \beta^{d} \in F$ .

Nel nostro caso le radici di $x^{p} - \beta = x^{p} - \alpha^{p}$ sono

$\displaystyle \alpha, \alpha \vartheta , \alpha \vartheta ^{2}, \dots, \alpha \vartheta ^{p-1},$

ove $\vartheta$ è una radice primitiva

-sima di

. Di queste, solo $\alpha$ è reale, e quindi se $x^{p} - \beta$ fosse riducibile otterremo l'assurdo $F = E = M = F(\alpha)$ .

Dunque $x^{p} - \beta$ è irriducibile su , e per ragioni di grado , e . Ma allora nell'estensione normale ci dovrebbero essere le altri radici di $x^{p} - \alpha^{p} = x^{3} - \alpha^{3}$ . Di nuovo, queste sono $\alpha, \alpha \omega, \alpha \omega^{2}$ , ove $\omega$ è una radice terza primitiva dell'unità, e quindi le altre due radici non sono reali, una contraddizione finale.

Un esempio

Un polinomio che dà luogo al casus irreducibilis è per esempio $f(x) = x^{3} - 6 x + 2$ , con $F = \mathbf{Q}$ . E' irriducibile in $\mathbf{Q}[x]$ , per il criterio di Eisenstein. Si ha

$\displaystyle \lim_{x \to - \infty} f(x) = -\infty, \qquad \lim_{x \to \infty} f(x) = \infty,$

. Dunque

ha tre radici reali.

$next$ $up$ $previous$ $contents$
Next: L'equazione di quarto grado Up: Le lezioni Previous: L'equazione di terzo grado Indice

A. Caranti
2000-05-31