



Next: Casus Irreducibilis
Up: Le lezioni
Previous: Equazioni risolubili per radicali
Indice
Subsections
Questa parte è presa quasi di peso da [vdW71].
Supponiamo sempre di essere in caratteristica zero.
Denotiamo con
![$ \Delta(t_{1}, t_{2}, \dots , t_{n}) \in \mathbf{Z}[t_{1},
t_{2}, \dots , t_{n}]$](img843.gif) l'elemento di (7.10.1). Il gruppo
simmetrico
l'elemento di (7.10.1). Il gruppo
simmetrico 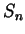 agisce su
agisce su
![$ \mathbf{Z}[t_{1}, t_{2}, \dots , t_{n}]$](img844.gif) permutando gli indici. Un 2-ciclo ha l'effetto di scambiare due
colonne della matrice di (7.10.1), e quindi di cambiare il
segno di
permutando gli indici. Un 2-ciclo ha l'effetto di scambiare due
colonne della matrice di (7.10.1), e quindi di cambiare il
segno di
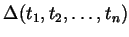 . Ne segue che
. Ne segue che
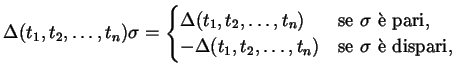 |
(8.1.1) |
Prendiamo adesso un'equazione di grado 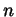 su un campo
su un campo 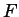 ,
,
e siano
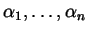 le sue radici nel campo di
spezzamento
le sue radici nel campo di
spezzamento 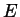 . Sia
. Sia
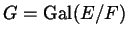 . Allora
. Allora
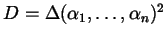 è fissato da
è fissato da 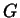 , e quindi sta in
, e quindi sta in 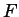 .
. 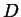 viene detto discriminante del polinomio o
dell'equazione. Per esempio, per l'equazione di secondo grado
viene detto discriminante del polinomio o
dell'equazione. Per esempio, per l'equazione di secondo grado
viene
proprio il discriminante noto. Infatti
In generale, dato che
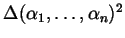 è
una funzione simmetrica degli
è
una funzione simmetrica degli
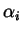 , si deve scrivere come un
polinomio nelle funzioni simmetriche elementari negli
, si deve scrivere come un
polinomio nelle funzioni simmetriche elementari negli
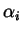 ,
cioè nei coefficienti
,
cioè nei coefficienti 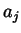 . Sia
. Sia
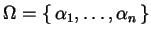 . Abbiamo già notato
in 3.3 che la restrizione
. Abbiamo già notato
in 3.3 che la restrizione
è un morfismo (ben definito e) iniettivo, per cui gli elementi del
gruppo di Galois possono essere visti come permutazioni su 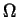 ,
ovvero come elementi di
,
ovvero come elementi di 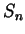 .
.
Lemma 1
Sono equivalenti
- Tutti gli elementi di
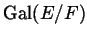 danno luogo a
permutazioni pari.
danno luogo a
permutazioni pari.
-
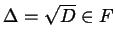 .
.
Dimostrazione.
Se tutte le permutazioni sono pari, allora
per (
8.1.1)
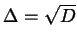
è fissato da ogni
elemento di
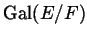
, e dunque è in
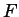
.
Viceversa se
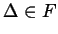 , allora
, allora 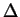 è fissato da ogni
elemento di
è fissato da ogni
elemento di 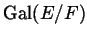 , e dunque per (8.1.1)
ogni tale elemento rappresenta una pernutazione pari.
, e dunque per (8.1.1)
ogni tale elemento rappresenta una pernutazione pari.
Veniamo adesso all'equazione di terzo grado
(le notazioni 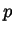 e
e 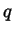 sono tradizionali), a cui supponiamo di aver
già rimosso col solito trucco il coefficiente di
sono tradizionali), a cui supponiamo di aver
già rimosso col solito trucco il coefficiente di 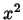 , e
prendiamola su un campo
, e
prendiamola su un campo 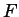 che contenga una radice terza
dell'unità
che contenga una radice terza
dell'unità
Ricordiamo che
Tanto vale supporre 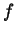 irriducibile su
irriducibile su 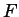 , altrimenti abbiamo
equazioni di grado uno o due, non tre. Dunque il gruppo di Galois
, altrimenti abbiamo
equazioni di grado uno o due, non tre. Dunque il gruppo di Galois
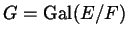 sarà
sarà 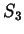 o
o 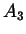 . Infatti sappiamo che il
gruppo di Galois è in grado di mandare ciascuna delle tre radici del
polinomio irriducibile
. Infatti sappiamo che il
gruppo di Galois è in grado di mandare ciascuna delle tre radici del
polinomio irriducibile 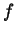 in ciascun'altra, ovvero come gruppo di
permutazioni deve essere transitivo sulle tre radici. Che i
sottogruppi transitivi di
in ciascun'altra, ovvero come gruppo di
permutazioni deve essere transitivo sulle tre radici. Che i
sottogruppi transitivi di 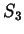 siano solo
siano solo 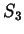 e
e 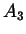 è ora
facile, dato che gli altri hanno ordine due, e scambiano fra loro due
radici, fissando la terza. In ogni caso alla catena di sottogruppi
è ora
facile, dato che gli altri hanno ordine due, e scambiano fra loro due
radici, fissando la terza. In ogni caso alla catena di sottogruppi
corrispondono i campi fissati
Quindi la prima estensione radicale è
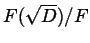 (di
grado uno o due), e si tratta di esprimere in forma radicale
l'estensione di grado tre
(di
grado uno o due), e si tratta di esprimere in forma radicale
l'estensione di grado tre
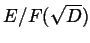 . Notate che questa è una
estensione normale, ed ha gruppo di Galois
. Notate che questa è una
estensione normale, ed ha gruppo di Galois 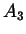 , quindi soddisfa le
ipotesi di 7.11.1.
, quindi soddisfa le
ipotesi di 7.11.1.
Con alcuni calcoli si può vedere [Jac85] che il discriminante
è
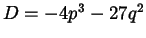 . Siano
. Siano
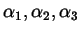 le tre radici. Formiamo i risolventi di Lagrange
le tre radici. Formiamo i risolventi di Lagrange
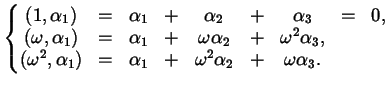 |
(8.2.1) |
Sappiamo che
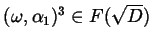 .
A questo proposito, vale la pena di notare che il più piccolo campo
su cui
.
A questo proposito, vale la pena di notare che il più piccolo campo
su cui  è definito è
è definito è
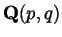 , per cui non si perde niente a
supporre
, per cui non si perde niente a
supporre
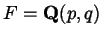 . Dunque
. Dunque
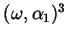 deve essere
esprimibile in termini di
deve essere
esprimibile in termini di
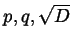 .
.
Per trovare questa
espressione in forma esplicita, calcoliamo
La formula per
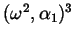 è del tutto analoga,
dato che basta (ovviamente!) scambiare
è del tutto analoga,
dato che basta (ovviamente!) scambiare 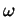 e
e
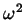 .
.
Ora
Se scriviamo temporaneamente
possiamo risolvere il sistema dato dalle ultime due equazioni, ed
ottenere
Ora possiamo riscrivere (8.3.1), tenendo conto che
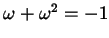 e
e
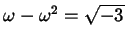 , come
, come
Ora vogliamo esprimere
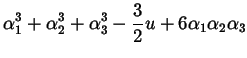 |
(8.3.2) |
in termini di
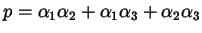 e
e
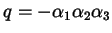 : si
deve poter fare, perché (8.3.2) è una funzione
simmetrica degli
: si
deve poter fare, perché (8.3.2) è una funzione
simmetrica degli
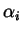 . Ricordiamo che
. Ricordiamo che
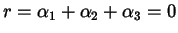 . Notiamo
. Notiamo
Se voglio ottenere un coefficiente 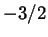 davanti a
davanti a 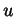 , posso
sottrarre dalla prima
, posso
sottrarre dalla prima 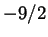 volte la seconda, ottenendo
volte la seconda, ottenendo
Basta solo aggiungere
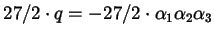 per ottenere complessivamente
per ottenere complessivamente
Quello che abbiamo fatto è un caso particolare di un algoritmo più
generale per esprimere una funzione polinomiale simmetrica in termini
di funzioni simmetriche elementari: vedi [vdW71].
La morale è che
e similmente
Prima di estrarre allegramente le radici cubiche, occorre notare che
bisogna farlo in modo coerente - una volta scelta la prima, la
seconda si determina tenendo presente che
Finalmente possiamo risolvere il sistema (8.2.1), dato
che conosciamo i termini di sinistra, e otteniamo
dove una volta scelta una delle tre radici cubiche possibili di
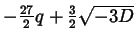 , dobbiamo quindi calcolare
la radice cubica di
, dobbiamo quindi calcolare
la radice cubica di
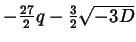 usando (8.3.3).
usando (8.3.3).




Next: Casus Irreducibilis
Up: Le lezioni
Previous: Equazioni risolubili per radicali
Indice
A. Caranti
2000-05-31
![]() l'elemento di (7.10.1). Il gruppo
simmetrico
l'elemento di (7.10.1). Il gruppo
simmetrico ![]() agisce su
agisce su
![]() permutando gli indici. Un 2-ciclo ha l'effetto di scambiare due
colonne della matrice di (7.10.1), e quindi di cambiare il
segno di
permutando gli indici. Un 2-ciclo ha l'effetto di scambiare due
colonne della matrice di (7.10.1), e quindi di cambiare il
segno di
![]() . Ne segue che
. Ne segue che
![]() su un campo
su un campo ![]() ,
,
![]() è
una funzione simmetrica degli
è
una funzione simmetrica degli
![]() , si deve scrivere come un
polinomio nelle funzioni simmetriche elementari negli
, si deve scrivere come un
polinomio nelle funzioni simmetriche elementari negli
![]() ,
cioè nei coefficienti
,
cioè nei coefficienti ![]() . Sia
. Sia
![]() . Abbiamo già notato
in 3.3 che la restrizione
. Abbiamo già notato
in 3.3 che la restrizione
![]() , allora
, allora ![]() è fissato da ogni
elemento di
è fissato da ogni
elemento di ![]() , e dunque per (8.1.1)
ogni tale elemento rappresenta una pernutazione pari.
, e dunque per (8.1.1)
ogni tale elemento rappresenta una pernutazione pari.
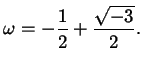
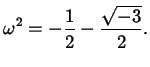
![]() irriducibile su
irriducibile su ![]() , altrimenti abbiamo
equazioni di grado uno o due, non tre. Dunque il gruppo di Galois
, altrimenti abbiamo
equazioni di grado uno o due, non tre. Dunque il gruppo di Galois
![]() sarà
sarà ![]() o
o ![]() . Infatti sappiamo che il
gruppo di Galois è in grado di mandare ciascuna delle tre radici del
polinomio irriducibile
. Infatti sappiamo che il
gruppo di Galois è in grado di mandare ciascuna delle tre radici del
polinomio irriducibile ![]() in ciascun'altra, ovvero come gruppo di
permutazioni deve essere transitivo sulle tre radici. Che i
sottogruppi transitivi di
in ciascun'altra, ovvero come gruppo di
permutazioni deve essere transitivo sulle tre radici. Che i
sottogruppi transitivi di ![]() siano solo
siano solo ![]() e
e ![]() è ora
facile, dato che gli altri hanno ordine due, e scambiano fra loro due
radici, fissando la terza. In ogni caso alla catena di sottogruppi
è ora
facile, dato che gli altri hanno ordine due, e scambiano fra loro due
radici, fissando la terza. In ogni caso alla catena di sottogruppi
![]() . Siano
. Siano
![]() le tre radici. Formiamo i risolventi di Lagrange
le tre radici. Formiamo i risolventi di Lagrange
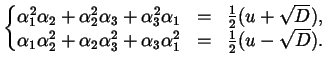
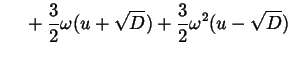
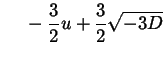
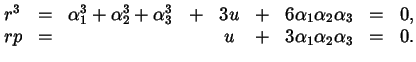
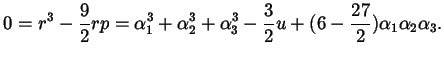
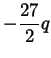
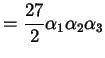
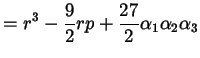
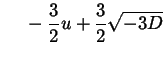
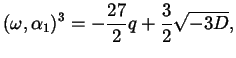
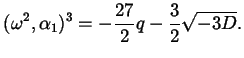
![\begin{displaymath}\begin{cases}3 \alpha_{1} = \sqrt[3]{- \frac{27}{2} q + \frac...
...[3]{- \frac{27}{2} q - \frac{3}{2} \sqrt{- 3 D}}\\ \end{cases}\end{displaymath}](img909.gif)