next up previous contents
Next: Numeri trascendenti Up: Le lezioni Previous: L'equazione di quarto grado   Indice

Subsections

Teoria di Galois delle estensioni di dimensione infinita

Questo capitolo trae origine da alcune note che avevo scritto per me stesso, e che ho rielaborato un po' per la prima versione (1997/98) di queste note. Nel 1998/99 non ho trattato questa parte, per cui non ho avuto occasione di rimetterci le mani, cosa che sarebbe ben necessaria. Mi riprometto di sistemarle decentemente la prossima volta.

Prendo sostanzialmente da [Lan84] l'estensione della teoria di [Kap95] dal caso delle estensioni di grado finito a quella delle estensioni algebriche, e svolgo l'esercizio [Lan84, n 19, p 233] indicatomi da Edoardo Ballico. Si può usare [Hig74] per i gruppi topologici, ma vedendo solo il minimo essenziale per capire ciò di cui si parla.

Si comincia definendo il campo di spezzamento di una famiglia qualsiasi di polinomi. L'esistenza deriva da fatti generali di teoria degli insiemi, che ometterei. Se si prendono in particolare tutti i polinomi (monici e) non costanti, si ottiene la chiusura algebrica come caso particolare.

Vale anche qui l'unicità, cioè è possibile estendere gli isomorfismi. Qui può valere la pena fare un argomento ``alla Zorn'', a scopo illustrativo. Per vedere che l'estensione è un isomorfismo, si ricorda il Lemma [Lan84, Lemma 1, p. 167], già visto a lezione, che dice che un isomorfismo di $ E / F$ in sé stesso, con $ E$ estensione algebrica di $ F$, è anche suriettivo. Si fa prendendo $ \alpha \in E$, e riducendosi a

$\displaystyle F (\alpha_{1}, \dots, \alpha_{n}),$    

ove gli $ \alpha_{i}$ sono le radici in $ E$ del polinomio minimo di $ \alpha$ su $ F$.

Ancora mediante il Lemma si estende al caso algebrico di grado arbitrario la caratterizzazione dei campi di spezzamento mediante il fatto che ogni polinomio irriducibile che vi ha una radice vi si spezza completamente.

Poi mostro l'equivalenza anche per un'estensione algebrica $ E / F$ delle condizioni:

$ (1) \Rightarrow (2)$ è come nel caso finito. $ (2) \Rightarrow (3)$ è ovvio, naturalmente. Si prova agevolmente anche $ (3) \Rightarrow (2)$, ricordando che $ E$ è l'unione insiemistica delle estensioni mediante le radici dei particolari polinomi di cui in $ (3)$, quindi tutte ``piccole'' estensioni normali, e pertanto separabili, per il solito Lemma.

Infine da $ (2)$ a $ (1)$ si passa mediante l'estendibilità degli automorfismi: tanto vale allora far vedere che ogni campo intermedio è chiuso.

Definizione di gruppo topologico, ed esempio dei numeri reali rispetto all'addizione. Topologia prodotto.

Comincio con il Lemma sul fatto che $ (x,y) \mapsto x \cdot y^{-1}$ è continua, e sul fatto che se $ V$ è aperto allora cè un aperto $ U$ tale che $ U \cdot U^{-1} \subseteq V$. Ne deduco che se è $ T_{1}$ (i punti sono chiusi) allora è anche $ T_{2}$.

Esercizio 11   Si mostri che se $ G$ è un gruppo, e anche uno spazio topologico, e la mappa

$\displaystyle G \times G$ $\displaystyle \to G$    
$\displaystyle (x,y)$ $\displaystyle \mapsto x \cdot y^{-1}$    

è continua allora $ G$ è un gruppo topologico.

Le traslazioni sono continue, dunque un gruppo topologico è uno spazio omogeneo, e per conoscerne la topologia basta conoscere gli aperti contenenti $ 1$, e anzi basta un sistema fondamentale, cioè gli elementi di una base che contengano $ 1$.

Ora prendo un'estensione algebrica e normale $ E / F$. Definisco la topologia di Krull sull'insieme $ E^{E} = \prod_{x in E} E_{x}$ delle mappe da $ E$ a $ E$. (Qui ogni $ E_{x}$ è una copia di $ E$, e la mappa $ f : E \to E$ corrisponde alla $ E$-pla $ (f(x))_{x \in E}$.) Questa è la topologia prodotto, ove $ E$ ha la topologia discreta.

La topologia di Krull ha dunque per base gli insiemi del tipo

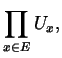$\displaystyle \prod_{x \in E} U_{x},$    

dove tutti gli $ U_{x}$ tranne un numero finito coincidono con $ E$, mentre quelli rimanenti sono aperti di $ E$, o anche basta aperti di base, e quindi sono della forma $ U_{x} = \{ y \}$, per qualche $ y \in E$.

Fissiamo un $ n \ge 1$, poi $ n$ punti distinti $ x_{1}, \dots x_{n} \in E$, e $ n$ punti arbitrari $ y_{1}, \dots y_{n} \in E$. Allora un aperto di base generico è dato da

$\displaystyle \left\{ f \in E^{E} : x_{i} g = y_{i}, i = 1, \dots , n \right\}.$    

(Perché basta prendere aperti di base, come detto.) Se prendo solo $ n = 1$ ottengo una sottobase. Istruttivo vedere chi sono gli aperti di base che contengono una funzione data: serve fra un attimo.

Questa topologia induce una struttura di gruppo topologico sull'insieme delle mappe biettive da $ E$ a $ E$, cioè rende continue le mappe prodotto e inversa. Questo si vede bene prendendo la sottobase della topologia prodotto su $ E^{E}$, dato che le immagini inverse conservano sia unione che intersezione. Si ha:

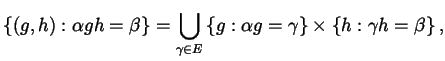$\displaystyle \left\{ (g,h) : \alpha g h = \beta \right\} = \bigcup_{\gamma \in... ...\{ g : \alpha g = \gamma \right\} \times \left\{ h : \gamma h = \beta \right\},$    

mentre per l'inversa ho

$\displaystyle \left\{ g : \alpha g^{-1} = \beta \right\} = \left\{ g : \beta g = \alpha \right\}$    

Notare chi sono gli aperti contenenti l'unità, avendo visto la cosa già per un elemento qualsiasi: ripetuto subito sotto.

Topologia di Krull sul gruppo di Galois

Ora, su $ G = \Gal ( E / F )$ definisco la topologia di Krull come ereditata dal gruppo delle mappe biettive da $ E$ a $ E$.

(Dubbio su quanto segue: Definire uno SFIA, le sue connessioni con la topologia, e vedere che il caso particolare di un insieme di sottogruppi (normali) a intersezione $ 1$ definisce una topologia che è Hausdorff, e totalmente sconnessa.)

Si vede subito che uno SFIA (sistema fondamentale di intorni aperti, vedi [Hig74]: basta dire che sono aperti di base contenenti $ 1$, e che determinano tutta la topologia, per la solita faccenda delle traslazioni) di $ 1$ è dato dalla famiglia dei sottogruppi $ K'$, ove $ K$ è un'estensione di dimensione finita di $ F$ in $ E$. Infatti un intorno di definizione è della forma

$\displaystyle \left\{ g \in G : \alpha_{i} g = \alpha_{i}, i = 1, \dots , n \right\} = F(\alpha_{1}, \dots, \alpha_{n})'.$    

Va anche bene prendere come SFIA di $ 1$ la famiglia di sottogruppi normali

$\displaystyle \mathcal{U} = \left\{ U = N' : \text{$N$\ estensione \emph{normale} di dimensione finita di $F$} \right\}.$    

Infatti se $ K = F(\alpha_{1}, \dots, \alpha_{n})$ come sopra, prendo la sua chiusura normale $ N$, che è ancora in $ E$ per quanto visto sopra. Dunque $ N' \le K'$, e quindi se è aperto il primo lo è anche il secondo, che ne è unione di classi laterali. (Un sottogruppo aperto è anche chiuso. Un sottogruppo che contenga un sottogruppo aperto è aperto.)

Chiuso nella topologia di Krull e chiuso nella corrispondenza di Galois

Ora dico che $ H \le G$ è Krull-chiuso sse $ H = H''$, cioè $ H$ è Galois-chiuso. Infatti, se $ H = L'$, allora

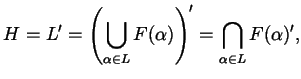$\displaystyle H = L' = \left( \bigcup_{\alpha \in L} F (\alpha) \right)' = \bigcap_{\alpha \in L} F (\alpha)',$    

e quindi è Krull-chiuso.

Nota che ho usato il Lemma immediato, in esercizio sul Kaplansky, che dice $ (L \cup M)' = (L \vee M)' = L' \cap M'$, valido anche nel caso di un numero arbitrario di termini. $ L \vee M$ sta per il compositum, cioè il sottocampo generato. Vale la pena di dire due parole sul caso algebrico, che è appena un po' più semplice, anche se a lezione ho fatto del tutto a meno del compositum.

Adesso mostro che Krull-chiuso implica Galois-chiuso. Noto prima la formula $ \overline{H} = \bigcap \{ H U : U \in \mathcal{U} \}$. Questa vale facilmente nel nostro contesto, dato che $ U = U^{-1}$ per i nostri sottogruppi $ U$. Nel caso di un gruppo topologico qualiasi, basta notare che se uno ha uno SFIA, si possono rimpiazzare i suoi elementi $ V$ con quelli $ U = V\cap V^{-1}$, e ora la formula vale rispetto a questi ultimi. Dunque $ a U^{-1} \cap H \ne \emptyset$ per ogni $ U \in \mathcal{U}$ sse $ a \in H U$ per ogni $ U \in \mathcal{U}$.

Ora se $ H = \overline{H}$ ho

$\displaystyle H = \overline{H} = \bigcap \{ H U : U \in \mathcal{U} \} = \bigcap \{ F_{U}' : U \in \mathcal{U} \} = ( \vee \{ F_{U} : U \in \mathcal{U} \} )',$    

ove $ \vee$ indica il compositum degli $ F_{U}$. (E' veramente necessario?) Qui si ha facilmente che $ H U = F_{U}$ per qualche campo intermedio $ F_{U}$, dato che $ U \le H U \le G$, $ U$ è Galois-chiuso, e l'indice $ \lvert G : U \rvert $ è finito, per cui anche quello $ \lvert HU : U \rvert $ lo è. Dunque, per il Lemma 3.9.2, anche $ H U$ è chiuso.

Cosa voglio fare adesso? Mostrare, credo, che il gruppo di Galois è compatto. Noto, se non l'ho fatto prima, che è $ T_{2}$, e totalmente sconnesso: per questo basta far vedere (vedi qui sotto) che $ \cap \, \mathcal{U} = \{ 1 \}$.

Immergo $ G$ nel suo completamento $ \mathcal{U}$-adico. Qui prendo $ \mathcal{U}$ una famiglia di sottogruppi normali con le proprietà:

Cominciamo col considerare il gruppo

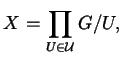$\displaystyle X = \prod_{U \in \mathcal{U}} G / U,$    

con la topologia prodotto, ove ogni $ G/U$ è (finito e) discreto. Nel nostro caso particolare $ \mathcal{U} = \left\{ U = N' : \hbox{$N$ estensione \emph{normale} di dimensione finita di $F$} \right\}$. Adesso consideriamo il sottogruppo di $ X$

$\displaystyle \widehat{G} = \{ (g_{U} U)_{U \in \mathcal{U}} :$   per $ U \ge V$ si ha $ g_{U} V = g_{V} V$$\displaystyle \}.$    

In altre parole, un elemento di $ X$ è una famiglia di automorfismi $ g_{L} \in \Gal (L / F)$, uno per ogni estensione normale $ L$ di $ F$ di grado finito. Una collezione di questo genere sta in $ \widehat{G}$ se vale che se $ L \supseteq M$, con $ L$ e $ M$ estensioni normali di $ F$ di grado finito, allora $ g_{L} \mid_{M} = g_{M}$. Una famiglia $ (g_{L})$ di questo tipo di dice compatibile.

Per vedere che sia isomorfo, è sufficiente vedere che l'immersione canonica

$\displaystyle \varphi :\ $ $\displaystyle G \to \widehat{G}$    
  $\displaystyle g \mapsto (g U)_{U \in \mathcal{U}}$    

sia suriettiva. In altre parole $ \varphi $ manda un elemento di $ \Gal(E/F)$ nell'insieme delle sue restrizioni alle estensioni normali di grado finito.

La suriettività segue dal fatto, veramente elementare, che una famiglia compatibile di automorfismi sulle estensioni normali, di dimensione finita, definisce un automorfismo di tutta l'estensione. Cioè che per ogni estensione normale di dimensione finita $ N/F$ ho un elemento $ g_{N} \in \Gal (N / F) \cong G / U$ tale che se $ N \supseteq M$ sono due estensioni di questo tipo allora

$\displaystyle g_{N} \mid_{M} = g_{M},$    

allora esiste $ g \in \Gal ( E/F )$ tale che

$\displaystyle g \mid _{N} = g_{N}$    

per ogni estensione normale di dimensione finita $ N/F$. Infatti per $ \alpha \in E$ definisco $ \alpha g$ come $ \alpha g_{N}$, ove $ N$ è la chiusura normale di $ F(\alpha)$. Si tratta di vedere che sia un automorfismo di $ E$.

Siano allora $ \alpha, \beta \in E$, e siano $ N$ la chiusura normale di $ F(\alpha)$, $ M$ la chiusura normale di $ F(\beta)$, e $ P \supseteq N \cup M$ la chiusura normale di $ F (\alpha, \beta)$. Per la condizione di compatibilità

$\displaystyle \alpha g = \alpha g_{N} = \alpha g_{P} \mid_{N} = \alpha g_{P},$    

e similmente $ \beta g = \beta g_{P}$. Dunque

$\displaystyle (\alpha + \beta) g = (\alpha + \beta) g_{P} = \alpha g_{P} + \beta g_{P} = \alpha g + \beta g,$    

e similmente per il prodotto.

Occorre poi vedere anche che $ \varphi $ sia un omeomorfismo, ma questo è abbastanza facile a partire dalle definizioni. La continuità è immediata, basta comporre con le proiezioni, e vedere che le controimmagini dei punti sono le classi laterali di uno dei sottogruppi di $ \mathcal{U}$. Vediamo ora che l'immagine di un aperto $ U \in \mathcal{U}$ è aperta in $ \widehat{G}$. Infatti l'immagine di $ U$ in $ \widehat{G}$ coincide con l'intersezione con $ \widehat{G}$ dell'aperto di sottobase che ha $ 1$ sulla componente $ U$-sima, e le altre componenti libere. Notate che non è detto che l'immagine in $ X$ di $ U$ sia aperta, dato che potrei star toccando infinite componenti contemporaneamente. (Espandere ancora un po'.)

Dovrei commentare che questo mostra la compattezza del gruppo di Galois, ma per questo devo notare che il sottogruppo di $ X$ è chiuso, cosa che non mi sembra abbia scritto finora. Questo deriva dal fatto che l'insieme delle famiglie compatibili è l'intersezione dei sottoinsiemi

$\displaystyle C = \left\{ (g_{L}) : g_{N} \mid_{M} = g_{M} \right\}$    

per fissati $ N \supseteq M$. Se mostriamo che ognuno di questi è chiuso siamo a posto, dato che ogni intersezione di chiusi è chiusa. Ora notiamo che $ C$ è un insieme riconducibile alla forma

$\displaystyle C = \left\{ x \in X : f(x) = g(x) \right\},$    

ove $ f, g: X \to Y$ sono mappe continue fra gli spazi topologici $ X$ e $ Y$. Qui $ X$ è il prodotto, e $ Y$ è $ \Gal(M/F)$. Le due mappe sono la proiezione su $ Y$, continua per definizione, e la composizione della proiezione su $ \Gal(N/F)$ (ancora continua) con la restrizione $ \Gal(M/F) \to \Gal(N/F)$, pure continua perché sono entrambi spazi discreti. Ora vale il Lemma, facile da dimostrare:

Lemma 1   $ Y$ è $ T_{2}$ se e solo se la diagonale

$\displaystyle \Delta = \{ (y, y) : y \in Y \} \subseteq Y \times Y$    

è chiusa in $ Y \times Y$.

Si conclude con l'osservazione che $ C$ è la controimmagine della diagonale $ \Delta \subseteq Y \times Y$ sotto la mappa

$\displaystyle X$ $\displaystyle \to Y \times Y$    
$\displaystyle x$ $\displaystyle \mapsto ( f(x), g(x)).$    

Quest'ultima mappa è continua perché le componenti lo sono per ipotesi. Dunque $ C$ è chiuso.

Un'osservazione finale

Ho da dimostrare il piccolo Lemma che se $ N$, $ M$ sono estensioni normali di $ F$, anche $ N \cap M$ lo è, ma questo mi pare sia chiaro attraverso i sottogruppi associati (prodotto di normali aperti), o anche mediante il Lemma che caratterizza le estensioni normali in base alle radici dei polinomi irriducibili (se ce n'è una ci sono tutte).

next up previous contents
Next: Numeri trascendenti Up: Le lezioni Previous: L'equazione di quarto grado   Indice
A. Caranti
2000-05-31