next up previous contents
Next: Estensioni normali e campi Up: Le lezioni Previous: Campo di spezzamento   Indice

Subsections

Corrispondenza di Galois

Il gruppo di Galois

Definiamo

\begin{equation*}\Gal ( E / F ) = \begin{aligned}[t]\{\, \varphi : E \to E : &\ ... ...&\ \text{$a \varphi = a$\ per ogni $a \in F$} \,\}. \end{aligned}\end{equation*}

$ \Gal(E/F)$ è detto il gruppo di Galois dell'estensione. Vi prego di verificare che è effettivamente un gruppo.

E' utile notare che nel caso particolare della Proposizione 2.2.4 in cui $ F = \overline{F}$, $ \bar{\cdot}$ è la mappa identica, e $ E_{1} = E_{2} = E$ è un fissato campo di spezzamento di $ f$ su $ F$, allora gli isomorfismi considerati sono in questo caso gli isomorfismi di $ E$ in se stesso (detti anche automorfismi di $ E$) che fissano ogni elemento di $ F$, cioè proprio gli elementi del gruppo di Galois.

Vediamo subito un esempio in cui il gruppo di Galois è banale. Prendiamo $ F = \mathbf{Q}$, e $ E = \mathbf{Q}[ \sqrt[3]{2} ]$. Dato che il polinomio minimo di $ \sqrt[3]{2}$ su $ \mathbf{Q}$ è $ x^{3} - 2$, ogni elemento di $ E$ si scrive in modo unico come

$\displaystyle a_{0} + a_{1} \sqrt[3]{2}+ a_{2} \sqrt[3]{2}^{2} \quad a_{i} \in \mathbf{Q},$    

e $ \lvert E : F \rvert = 3$. Sia adesso $ \varphi $ un elemento di $ \Gal(E/F)$. Dato che $ \varphi $ è un morfismo, e fissa gli elementi di $ \mathbf{Q}$. abbiamo

$\displaystyle ( a_{0} + a_{1} \sqrt[3]{2}+ a_{2} \sqrt[3]{2}^{2} ) \varphi = a_{0} + a_{1} (\sqrt[3]{2} \varphi ) + a_{2} (\sqrt[3]{2} \varphi )^{2}.$    

Dunque $ \varphi $ è determinato dal valore $ \sqrt[3]{2} \varphi $. Ora abbiamo $ (\sqrt[3]{2})^{3} - 2 = 0$. Applicando $ \varphi $ abbiamo

$\displaystyle (\sqrt[3]{2} \varphi )^{3} - 2 = 0,$    

cioè $ \sqrt[3]{2} \varphi \in E$ è ancora una radice di $ x^{3} - 2$. Ma le radici di questo polinomio sono

$\displaystyle \sqrt[3]{2},\quad \sqrt[3]{2} \cdot \left( \frac{-1 - i \sqrt{3}}{2} \right),\quad \sqrt[3]{2} \cdot \left( \frac{-1 + i \sqrt{3}}{2} \right),$    

ove i due numeri complessi sono le due radici terze dell'unità diverse da $ 1$, ovvero le radici di $ x^{2} + x + 1 = (x^{3} - 1) / (x - 1)$. Delle tre radici, solo la prima è reale, e quindi le altre due non stanno in $ E \subseteq \mathbf{R}$. La morale è che l'unica scelta possibile per $ \sqrt[3]{2} \varphi $ è $ \sqrt[3]{2}$, e dunque l'unica scelta possibile per $ \varphi $ è la mappa identica. Dunque $ \Gal(E/F)$ ha un unico elemento, mentre il grado $ \lvert E : F \rvert $ è $ 3$.

Più in generale, abbiamo visto nell'Esercizio 4 che ogni elemento di $ E = F (\alpha_{1}, \dots, \alpha_{n})$ è un polinomio begli $ \alpha_{i}$. Ne segue che un elemento di $ \Gal(E/F)$ è determinato dalla sua azione su $ \alpha_{1}, \dots, \alpha_{n}$, e che l'immagine sotto $ \varphi $ di $ \alpha_{i}$ deve essere una radice del polinomio minimo di $ \alpha_{i}$ su $ F$ che sia contenuta in $ E$.

In altre parole

Lemma 1   Sia $ E / F$ una estensione, $ f \in F[x]$ un polinomio monico e irriducibile. Sia $ \alpha \in E$ una radice di $ F$. Dunque $ f$ è il polinomio minimo di $ \alpha$ su $ F$.

Sia $ \varphi : E \to E$ un isomorfismo che ristretto a $ F$ induca la mappa identica.

Allora l'immagine $ \alpha \varphi $ di $ \alpha$ sotto $ \varphi $ è ancora una radice di $ f$.

In realtà il risultato vale anche se $ f$ non è irriducibile, ma vogliamo sottolineare il fatto che tanto $ \varphi $ non può mandare $ \alpha$ in nient'altro che altre radici del suo polinomio minimo.

Dimostrazione. Facile: scriviamo esplicitamente

$\displaystyle f = a_{0} + a_{1} x + \dots + a_{n-1} x^{n-1} + x^{n},$    

con $ a_{i} \in F$. Abbiamo

$\displaystyle 0 = f (\alpha) = a_{0} + a_{1} \alpha + \dots + a_{n-1} \alpha^{n-1} + \alpha^{n}.$    

Applichiamo $ \varphi $, tenendo presente che è un morfismo, e che $ a \varphi = a$ per ogni $ a \in F$, ottenendo proprio

$\displaystyle 0 = a_{0} + a_{1} ( \alpha \varphi ) + \dots + a_{n-1} ( \alpha \varphi )^{n-1} + ( \alpha \varphi )^{n} = f ( \alpha \varphi ).$    

Esercizio 7 (I dettagli li vedremo a lezione)  

Costruire i campi di spezzamento $ E_{1}$ di $ (x^{2} - 2) (x^{2} - 3)$ su $ \mathbf{Q}$ e $ E_{2}$ di $ x^{3} - 2$ su $ \mathbf{Q}$. Si tratta quindi di estensioni normali.

Si calcolino i gruppi di Galois $ \Gal ( E_{i} / \mathbf{Q})$, si costruiscano tutti i sottogruppi e campi intermedi, e si determini esplicitamente la corrispondenza di Galois.

La corrispondenza di Galois

Sia $ E / F$ una qualsiasi estensione di campi. (Potrebbe ben essere di grado infinito, o non algebrica.) Sia $ G = \Gal ( E / F )$ il gruppo di Galois. Consideriamo l'insieme $ \mathcal{H}$ dei sottogruppi di $ G$, e l'insieme $ \mathcal{L}$ dei campi $ L$ cosiddetti intermedi, $ F \subseteq L \subseteq E$. Definiremo due mappe con lo stesso nome ``primo'', una da $ \mathcal{H}$ a $ \mathcal{L}$, e una viceversa da $ \mathcal{L}$ a $ \mathcal{H}$.

La mappa $ ' : \mathcal{H}\to \mathcal{L}$ è definita, cosí, per $ H \in \mathcal{H}$,

$\displaystyle H' = \left\{\, a \in E : \text{$a h = a$\ per ogni $h \in H$} \,\right\}.$ (3.2.1)

Cioè $ H'$ consiste degli elementi di $ F$ che sono fissati da ogni elemento di $ H$. E' facile, ma istruttivo, vedere che $ H'$ sia in effetti un sottocampo di $ E$. Notate che ogni elemento di $ G$ fissa ogni elemento di $ F$, per la definizione (3.1.1) di $ G = \Gal ( E / F )$, e dunque ogni elemento di $ H \le G$ fa altrettanto. Dunque $ H' \supseteq F$, e quindi $ H' \in \mathcal{L}$.

Viceversa la mappa $ ' : \mathcal{L}\to \mathcal{H}$ è definita, per $ L \in \mathcal{L}$, mediante

$\displaystyle L' = \left\{\, g \in G : \text{$a g = a$\ per ogni $a \in L$} \,\right\}.$ (3.2.2)

Qui $ L'$ è quindi l'insieme degli elementi di $ G$ che fissano ogni elementi di $ L$. Di nuovo, è facile ma istruttivo verificare che $ L'$ è un sottogruppo di $ G$.

Cominciamo col vedere che succede ad applicare il ``primo'' agli oggetti $ E$, $ F$, $ \{ 1 \}$ e $ G$, ove $ \{ 1 \}$ è il sottogruppo di $ G$ consistente del solo elemento neutro $ 1$, ovvero della mappa identica su $ E$.

Si ha $ E' = \left\{\, g \in G : \text{$a g = a$\ per ogni $a \in E$} \,\right\} = \{ 1 \}$. dato che gli elementi di $ G$ sono automorifsmi di $ E$, ovvero mappe da $ E$ ad $ E$, e l'unica mappa che fissi tutti gli elementi di $ E$ è proprio la mappa identica.

Sia ha poi $ F' = \left\{\, g \in G : \text{$a g = a$\ per ogni $a \in F$} \,\right\} = G$, dato che per la definizione (3.1.1) tutti gli elementi di $ G$ fissano tutti gli elementi di $ F$.

Ancora, si ha immediatamente $ \{ 1 \}' = \left\{\, a \in E : \text{$a 1 = a$} \,\right\} = E$.

Invece quando si considera $ G' = \left\{\, a \in E : \text{$a g = a$\ per ogni $g \in G$} \,\right\} $ abbiamo un problema. Per completezza ci si aspetterebbe $ G' = F$. Ma mentre è chiaro che $ G' \supseteq F$, dato che ogni elemento di $ G$ fissa ogni elemento di $ F$, per la solita definizione (3.1.1), ma nell'esempio $ F = \mathbf{Q}$, $ E = \mathbf{Q} ( \sqrt[3]{2} )$ si ha $ G = \Gal ( E / F ) = \{ 1 \}$, e dunque $ G' = \{ 1 \}' = E \ne F$.


Gruppo di Galois e gruppo simmetrico

Finiamo l'esercizio 7, calcolando $ \Gal ( \mathbf{Q}( \sqrt[3]{2} , \omega) / \mathbf{Q})$, ove $ \omega^{2} + \omega + 1 = 0$. Questo è il campo di spezzamento su $ \mathbf{Q}$ di $ x^{3} - 2$. Fra le altre cose, si nota che il gruppo di Galois viene rappresentato come gruppo di permutazioni sulle radici di $ x^{3} - 2$, e dunque il gruppo in questo caso viene isomorfo a $ S_{3}$.. Prefiguriamo quindi il seguente argomento generale.

Sia $ F$ un campo, $ f \in F[x]$ monico e non costante. Sia $ E$ il campo di spezzamento di $ f$ su $ F$, sia $ G = \Gal ( E / F )$, e sia $ \Omega = \left\{\, \alpha_{1}, \dots, \alpha_{n} \,\right\}$ le radici di $ f$ in $ E$. Per il Lemma 3.1.1, ogni elemento di $ G$ manda elementi di $ \Omega$ in elementi di $ \Omega$. E' dunque definita una mappa

$\displaystyle \varphi :\ $ $\displaystyle G \to S ( \Omega )$    
  $\displaystyle g \mapsto (\alpha \to \alpha g).$    

Qui $ S (\Omega)$ è il gruppo delle permutazioni sull'insieme $ \Omega$. Per la parte finale dell'Esercizio 4, ogni elemento di $ E$ si scrive come una espressione polinomiale negli $ \alpha_{i}$. Dunque un elemento di $ G$ è determinato dalla sua azione sugli $ \alpha_{i}$. In altre parole la mappa $ \varphi $ è iniettiva. Abbiamo dunque ottenuto

Proposizione 1   Il gruppo di Galois di un campo di spezzamento è isomorfo a un gruppo di permutazioni sull'insieme delle radici.

Estensioni normali

Sia $ E / F$ una estensione, $ G = \Gal ( E / F )$, e consideriamo la corrispondenza di Galois. Sia $ L$ un campo intermedio. Notiamo che $ L' = \Gal (E/L)$.

Ora, la condizione che $ G' = F$ è proprio cruciale. Introduciamo la seguente definizione.

Definizione 1   L'estensione $ E / F$ si dice normale (o si dice anche che $ E$ è normale su $ F$) quando vale $ \Gal ( E / F)' = F$.

A parole (la prima volta fa girare un po' la testa), un'estensione $ E / F$ è normale quando i soli elementi di $ E$, che siano fissati da tutti gli automorfismi di $ E$ che fissano tutti gli elementi di $ F$, sono proprio gli elementi di $ F$. In generale potrebbero essercene di più, come mostra l'esempio appena visto di $ \mathbf{Q}( \sqrt[3]{2} ) / \mathbf{Q}$.

Daremo tra poco due risultati di base che ci permetteranno di comprendere bene la struttura delle estensioni normali. Cominciamo con alcune osservazioni elementari, ma che la prima volta richiedono un po' di riflessione. Siano $ H \le K \le G$ due sottogruppi di $ G$ uno dentro l'altro. Allora $ H' \supseteq K'$. Infatti ogni elemento di $ E$ che sia fissato da ogni elemento di $ K$ è in particolare fissato da ogni elemento di $ H \le K$. Similmente (istruttivo esercizio) se $ F \subseteq L \subseteq M \subseteq E$, allora $ L' \ge M'$. Non è poi difficile (ma ancora istruttivo) vedere che

$\displaystyle X'' \supseteq X$   se $ X \in \mathcal{H}$, o $ X \in \mathcal{L}$. (3.4.1)

A questo punto possiamo fare un'osservazione del tutto formale. Applicando di nuovo il primo abbiamo $ X''' \subseteq X'$. D'altra parte applicando (3.4.1) con $ X'$ al posto di $ X$ otteniamo $ X''' \supseteq X'$, e dunque $ X''' = X'$.

Notiamo che qualunque sia $ E / F$, l'estensione $ E/F'' = E/G'$ è sempre normale. Infatti si ha $ \Gal(E/F'') = F''' = F' = \Gal (E/F) = G$, e quindi $ \Gal(E/F'')' = G' = F''$. Questo è un modo, che utilizzeremo più avanti, per rimediare alla non normalità di certe estensioni. Naturalmente il risultato può essere deludente, ad esempio se si parte da $ F = \mathbf{Q}$ e $ E = \mathbf{Q}(\sqrt [3]{2})$, si ottiene $ F'' = \mathbf{Q}(\sqrt [3]{2})$, e banalmente l'estensione $ E/E$ è normale. Vedremo che c'è una ricetta ben più intelligente per passare da una estensione non normale a una normale, quando possibile.

Sottogruppi e campi intermedi chiusi

Introduciamo ora una terminologia di sapore topologico; per ora è solo una questione di parole, ma vedremo verso la fine del corso che corrisponde veramente a questioni topologiche. Diciamo che $ X \in \mathcal{H} \cup \mathcal{L}$ è chiudo nella corrispondenza di Galois se $ X'' = X$. Dunque se $ X$ è chiuso si ha $ X = (X')'$, cioè $ X$ è il primo di qualcosa. Viceversa, se $ X = Y'$ per qualche $ Y$, otteniamo $ X'' = Y''' = Y' = X$, e quindi $ X$ è chiuso. Quindi essere chiuso vuol dire esattamente essere il primo di qualcosa.

$ X''$ viene detto la chiusura di $ X$. In effetti $ X''$ è chiuso, ed è il minimo oggetto chiuso che contenga $ X$. Infatti se $ Y$ è chiuso, e $ X \subseteq Y$, allora $ X'' \subseteq Y'' = Y$.

Notiamo ancora che dire che $ F$ è chiuso significa $ F = F'' = G'$, ciè che $ E / F$ è normale.

Enunciamo adesso un primo risultato sulla corrispondenza di Galois fra sottogruppi e campi intermedi. Per ora si tratta di un risultato povero di significato, finché non abbiamo criteri per decidere quanti e quali oggetti siano chiusi.

Teorema 1 (Corrispondenza di Galois I)   Sia $ E / F$ una estensione, e sia $ G = \Gal ( E / F )$ il suo gruppo di Galois.

Allora le operazioni ``primo'' stabiliscono una corrispondenza biunivoca fra gli oggetti chiusi di $ \mathcal{H}$ e $ \mathcal{L}$.

La dimostrazione l'abbiamo in realtà già vista. Infatti il primo di qualsiasi cosa è un oggetto chiuso, e per un oggetto chiuso $ X$ vale $ X = X''$, cioè le due mappe primo sono una l'inversa dell'altra.

Lo strumento fondamentale per individuare oggetti chiusi sono Lemmi, che forniscono due diseguaglianze chiave.

Una diseguaglianza

Lemma 1   Sia $ E / F$ un'estensione, e consideriamo due campi intermedi uno dentro l'altro

$\displaystyle F \subseteq L \subseteq M \subseteq E.$    

Supponiamo che il grado $ \lvert M : L \rvert $ sia finito. Allora anche l'indice $ \lvert L' : M' \rvert $ è finito, e si ha

$\displaystyle \lvert M : L \rvert \ge \lvert L' : M' \rvert .$    

Un caso particolare utile di questo lemma è la seguente stima, se il grado $ \lvert E : F \rvert $ è finito

$\displaystyle \lvert E : F \rvert \ge \lvert F' : E' \rvert = \lvert G : \{ 1 \} \rvert = \left\lvert G \right\rvert .$ (3.6.1)

Dimostrazione. Procedendo per induzione sul grado dell'estensione, come in [Kap95, Theorem 6], si vede subito che si può supporre $ M = L ( \alpha )$, per qualche $ \alpha$.

Supponiamo infatti che esista un campo intermedio $ K$ fra $ L$ e $ M$, con $ K \ne L, M$. Per induzione, si ha

$\displaystyle \lvert K : L \rvert \ge \lvert L' : K' \rvert , \qquad \lvert M : K \rvert \ge \lvert K' : M' \rvert .$    

Usando la formula dei gradi e qualcosa del genere del teorema di Lagrange (vedi la Proposizione 3.7.3 subito dopo la fine di questa dimostrazione) si ottiene

$\displaystyle \lvert M : L \rvert = \lvert M : K \rvert \cdot \lvert K : L \rvert \ge \lvert K' : M' \rvert \cdot \lvert L' : K' \rvert = \lvert L' : M' \rvert .$    

Allora non vi sono campi intermedi fra $ L$ ed $ M$. Se ora $ \alpha \in M \setminus L$, si ha $ L(\alpha) \ne L$, e dunque $ L(\alpha) = M$.

Sia $ f \in L[x]$ il polinomio minimo di $ \alpha$ su $ L$, e sia $ \Omega$ l'insieme delle radici di $ f$ in $ M$. Chiaramente abbiamo $ \left\lvert \Omega \right\rvert \le \grado(f) = \lvert M : L \rvert $.

Ora per un argomento già visto $ L'$ agisce su $ \Omega$, dato che manda una radice di $ f$ in un'altra radice di $ f$. Lo stabilizzatore di $ \alpha$ quest'azione è $ M'$, dato che fissare $ \alpha$ equivale a fissare tutto $ M = L ( \alpha )$. Dunque per il Teorema orbita-stabilizzatore si ha che $ \lvert L' : M' \rvert $ è eguale alla grandezza dell'orbita di $ \alpha$ sotto $ L'$. Ma quest'orbita è contenuta in $ \Omega$. e quindi questo numero è minore di $ \lvert M : L \rvert $, come richiesto.

Un commento sul Teorema di Lagrange

La forma tradizionale è

Teorema 1 (Lagrange)   Sia $ G$ un gruppo finito, e $ H \le G$. Allora

$\displaystyle \left\lvert G \right\rvert = \left\lvert H \right\rvert \cdot \lvert G : H \rvert .$    

Qui $ \lvert G : H \rvert $ indica il numero di classi laterali di $ H$ in $ G$. Una facile conseguenza è

Corollario 2   Sia $ G$ un gruppo finito, e $ H \le K \le G$. Allora

$\displaystyle \lvert G : H \rvert = \lvert G : K \rvert \cdot \lvert K : H \rvert .$    

Basta calcolare, usando tre volte il Teorema di Lagrange

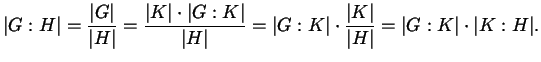$\displaystyle \lvert G : H \rvert = \frac{\left\lvert G \right\rvert }{\left\lv... ...{\left\lvert H \right\rvert } = \lvert G : K \rvert \cdot \lvert K : H \rvert .$    

In realtà vale un risultato appena un po' più generale, che abbiamo usato nella dimostrazione del Lemma 3.6.1. Enunciato e dimostrazione somigliano molto alla formula dei gradi.

Proposizione 3   Sia $ G$ un gruppo qualsiasi, e $ H \le K \le G$.
  1. Se il numero $ \lvert G : H \rvert $ di classi laterali di $ H$ in $ G$ è finito, allora sono finiti anche $ \lvert G : K \rvert $ e $ \lvert K : H \rvert $.
  2. Se sono finiti i numeri $ \lvert G : K \rvert $ e $ \lvert K : H \rvert $, allora anche $ \lvert G : H \rvert $ è finito.
  3. Se i tre numeri sono finiti, allora vale

    $\displaystyle \lvert G : H \rvert = \lvert G : K \rvert \cdot \lvert K : H \rvert .$    

Dimostrazione. Le classi laterali di $ H$ in $ K$ sono un sottonsieme delle classi laterali di $ H$ in $ G$, per cui che $ \lvert K : H \rvert $ sia finito è chiaro. Consideriamo la mappa

$\displaystyle g H \mapsto g K,$    

che associa a ogni classe laterale di $ H$ in $ G$ una classe laterale di $ K$ in $ G$. Si tratta di una mappa ben definita perché se $ g_{1} H = g_{2} H$ allora $ g_{1}^{-1} g_{2} \in H \le K$, e dunque $ g_{1} K = g_{2} K$. Dato che la mappa è ovviamente suriettiva, abbiamo anche qui che $ \lvert G : K \rvert $ è finito.

Ora resta da notare che se

$\displaystyle g_{1} K, g_{2} K, \dots, g_{n} K$    

sono le classi laterali distinte di $ K$ in $ G$, e

$\displaystyle k_{1} H, k_{2} H, \dots, k_{m} H$    

sono le classi laterali distinte di $ H$ in $ K$, allora

$\displaystyle g_{i} k_{j} H, \qquad 1 \le i \le n, 1 \le j \le m,$    

sono le classi laterali distinte di $ H$ in $ G$.

Infatti esauriscono certamente tutto $ G$, dato che

$\displaystyle G$ $\displaystyle = \bigcup \left\{\, g_{i} K : 1 \le i \le n \,\right\}$    
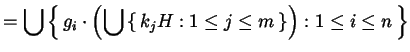  $\displaystyle = \bigcup \left\{\, g_{i} \cdot \left( \bigcup \left\{\, k_{j} H :1 \le j \le m \,\right\} \right) : 1 \le i \le n \,\right\}$    
  $\displaystyle = \bigcup \left\{\, g_{i} k_{j} H : 1 \le i \le n, 1 \le j \le m \,\right\}.$    

Vediamo che sono distinte fra loro. Se $ g_{i} k_{j} H = g_{i'} k_{j'} H$, allora $ k_{j}^{-1} g_{i}^{-1} g_{i'} k_{j'} \in H \le K$. In particolare $ g_{i}^{-1} g_{i'} \in k_{j} K k_{j'}^{-1} = K$, e dunque $ g_{i} = g_{i'}$. A questo punto $ k_{j} H = k_{j'} H$, e quindi anche $ k_{j} = k_{j'}$.

Un'altra diseguaglianza

Lemma 1   Sia $ E / F$ un'estensione, e $ G = \Gal ( E / F )$. Siano $ H \le K \le G$ sottogruppi di $ G$ uno dentro l'altro.

Supponiamo che l'indice $ \lvert K : H \rvert $ sia finito. Allora anche il grado $ \lvert H' : K' \rvert $ è finito, e si ha

$\displaystyle \lvert K : H \rvert \ge \lvert H' : K' \rvert .$    

La dimostrazione è ripresa da [Kap95, Theorem 7].

Dimostrazione. Per ogni $ \alpha \in H'$, e $ k \in K$, si può considerare l'elemento $ \alpha k$, che in generale sarà in $ E$, non necessariamente ancora in $ H'$. Se poi $ h \in K$, chiaramente $ \alpha h = \alpha$. Dunque se $ k_{1}, k_{2} \in K$ sono elementi nella stessa classe laterale $ H k_{1} = H k_{2}$, si ha $ k_{1} = h k_{2}$ per qualche $ h \in H$, e quindi per ogni $ \alpha \in H'$ vale

$\displaystyle \alpha k_{1} = \alpha h k_{2} = \alpha k_{2}.$    

In altre parole, si può definire in modo non ambiguo, per ogni $ k \in K$, l'azione $ \alpha (H k) = \alpha k$ della classe laterale $ H k$ di $ K$ rispetto ad $ H$ su ogni $ \alpha \in H'$.

Supponiamo adesso per assurdo che sia $ n = \lvert K : H \rvert < \lvert H' : K' \rvert $. Siano $ \alpha_{1}, \alpha_{2}, \dots, \alpha_{n+1} \in H'$ indipendenti su $ K'$. Siano $ \tau_{1}, \dots, \tau_{n}$ le classi laterali di $ H$ in $ K$ - diciamo che sia $ \tau_{1} = H$. Consideriamo il sistema di $ n$ equazioni lineari nelle $ n+1$ incognite $ x_{1}, \dots, x_{n+1}$:

$\displaystyle \left\{ \begin{matrix}x_{1} \cdot (\alpha_{1} \tau_{1}) & + & x_{... ... \dots & + & x_{n+1} \cdot (\alpha_{n+1} \tau_{n}) & = & 0 \end{matrix} \right.$ (3.8.1)

Dato che è un sistema di $ n$ equazioni lineari omogenee in $ n+1$ incognite c'è senz'altro una soluzione $ x_{1}, \dots, x_{n+1} \in E$, con gli $ x_{i}$ non tutti nulli. Prendiamone una in cui il numero $ r$ di $ x_{i}$ diversi da zero sia minimo. Scambiando fra loro gli $ x_{i}$, possiamo senz'altro supporre che sia $ x_{1} \ne 0, x_{2} \ne 0, \dots, x_{r} \ne 0$, e $ x_{r+1} = \dots = x_{n+1} = 0$. Dato che il sistema è omogeneo, possiamo anche moltiplicare la soluzione per $ x_{1}^{-1}$, e assumere quindi $ x_{1} = 1$.

Se fosse $ x_{i} \in K'$ per ogni $ i$, avrei già ottenuto una contraddizione. Infatti $ \tau_{1} = H$, e dunque per ogni $ \alpha_{i} \in H'$ avrei $ \alpha_{i} \tau_{1} = \alpha_{i} H = \alpha_{i}$, per cui la prima equazione di (3.8.1) diventa

$\displaystyle x_{1} \cdot \alpha_{1} + x_{2} \cdot \alpha_{2} + \dots + x_{n+1} \cdot \alpha_{n+1} = 0.$    

Questa sarebbe una relazione di dipendenza lineare su $ K'$ degli $ \alpha_{i}$, contro l'ipotesi.

Dunque uno degli $ x_{i}$ non sarà in $ K'$. Al solito, scambiando gli indici, possiamo supporre che sia $ x_{2} \not\in K'$. Dunque esisterà $ k \in K$ tale che $ x_{2} k \ne x_{2}$. Applichiamo $ k$ a tutte le equazioni in (3.8.1). Otteniamo

$\displaystyle \left\{ \begin{matrix}(x_{1} k) \cdot (\alpha_{1} \tau_{1} k) & +... ... & + & (x_{n+1} k) \cdot (\alpha_{n+1} \tau_{n} k) & = & 0 \end{matrix} \right.$ (3.8.2)

Ora se $ \tau_{1}, \dots, \tau_{n}$ sono le classi laterali di $ H$ in $ K$, la moltiplicazione per $ k$ (a destra) non fa altro che permutarle. Dunque $ \tau_{1} k, \dots, \tau_{n} k$ sono ancora le classi laterali di $ H$ in $ K$, magari in un ordine diverso. Ma allora la matrice dei coefficienti del sistema (3.8.2) è la stessa di quella del sistema (3.8.1): è solo che le righe sono scambiate. Dunque in (3.8.2) c'è scritto che oltre a

$\displaystyle x_{1}, x_{2}, \dots, x_{r}, 0, \dots, 0,$    

anche

$\displaystyle x_{1} k, x_{2} k, \dots, x_{r} k, 0, \dots, 0$    

è una soluzione di (3.8.1). Dato che si tratta di un sistema omogeneo, anche la differenza

$\displaystyle x_{1} - x_{1} k, x_{2} - x_{2} k, \dots, x_{r} - x_{r} k, 0, \dots, 0$ (3.8.3)

è una soluzione. Non si tratta della soluzione fatta di tutti zeri, perché abbiamo visto che $ x_{2} - x_{2} k \ne 0$. Però dato che $ x_{1} = 1$, si ha $ x_{1} - x_{1} k = 1 - 1 k = 0$. Dunque la soluzione (3.8.3) ha un numero di componenti non nulle minore di quello di $ x_{1}, x_{2}, \dots, x_{r}, 0, \dots, 0$. Questa è una contraddizione.

Oggetti chiusi in estensioni di grado finito

Otteniamo subito il seguente importante

Corollario 1   Sia $ E / F$ un'estensione, e $ G = \Gal ( E / F )$.
  1. I sottogruppi finiti di $ G$ sono chiusi.
  2. Se $ E / F$ è normale, e $ L$ è un campo intermedio tale che $ \lvert L : F \rvert $ sia finito, allora $ L$ è chiuso.

Dimostrazione. Sia $ H \le G$ di ordine finito. Allora

\begin{multline*} \left\lvert H \right\rvert = \lvert H : \{ 1 \} \rvert \ge \l... ...= \lvert H'' : \{ 1 \} \rvert = \left\lvert H'' \right\rvert . \end{multline*}

D'altra parte $ H \le H''$, e dunque $ \left\lvert H \right\rvert \le \left\lvert H'' \right\rvert $, per cui $ H = H''$.

Per la seconda parte,

$\displaystyle \lvert L : F \rvert \ge \lvert F' : L' \rvert = \lvert G : L' \rvert \ge \lvert L'' : G' \rvert = \lvert L'' : F \rvert ,$    

ove abbiamo usato il fatto che $ G' = \{ 1 \}$, cioè la normalità di $ E / F$. Come prima $ L \subseteq L''$, e dunque $ \lvert L : F \rvert = \lvert L'' : F \rvert $. Quindi $ L$ e $ L''$ sono due spazi vettoriali su $ F$ della stessa dimensione finita, uno contenuto nell'altro. Dunque $ L = L''$.

E' istruttivo considerare la dimostrazione dell'equivalente della seconda affermazione del Corollario 3.9.1 nel caso dei gruppi. (Ciò costituisce una affermazione più generale della prima del Corollario 3.9.1.) Cioè

Lemma 2   Se $ H \le K \le G$, l'indice $ \lvert K : H \rvert $ è finito, e $ H$ è chiuso, allora $ K$ è chiuso.

Dimostrazione. Come nel caso dei campi, arriviamo a

$\displaystyle \lvert K : H \rvert = \lvert K'' : H \rvert ,$   e$\displaystyle \qquad K \subseteq K''.$    

Se $ K$ fosse finito, dedurremmo subito da Lagrange che $ K$ e $ K''$ hanno lo stesso ordine, e dunque coincidono. In generale, basta comunque notare che $ K$ è unione di $ \lvert K : H \rvert $ classi laterali di $ H$, e $ K'' \supseteq K$ è unione dello stesso numero di classi laterali di $ H$: dunque le prime esauriscono già $ K''$, e quindi $ K = K''$.

Otteniamo subito

Teorema 3 (Teorema fondamentale della teoria di Galois)  

Sia $ E / F$ una estensione normale di grado finito, e $ G = \Gal ( E / F )$.

Allora tutti i sottogruppi di $ G$ e i sottocampi intermedi sono chiusi nella corrispondenza di Galois, e le operazioni ``primo'' stabiliscono una corrispondenza biunivoca fra i due insiemi.

Tali corrispondenze mandano gradi di campi in indici di sottogruppi e viceversa. In particolare

$\displaystyle \left\lvert G \right\rvert = \lvert E : F \rvert .$    

Dimostrazione. Resta solo da vedere l'ultima affermazione. Per sempio se $ F \subseteq L \subseteq M \subseteq E$, abbiamo

$\displaystyle \lvert M : L \rvert \ge \lvert L' : M' \rvert \ge \lvert M'' : L'' \rvert = \lvert M : L \rvert ,$    

dove l'ultima eguaglianza segue dal fatto che $ L$ e $ M$ sono chiusi. Dunque otteniamo $ \lvert M : L \rvert = \lvert L' : M' \rvert $. In particolare

$\displaystyle \lvert E : F \rvert = \lvert F' : E' \rvert = \lvert G : \left\{\, 1 \,\right\} \rvert = \left\lvert G \right\rvert ,$    

dove $ F' = G$ è l'ipotesi di normalità.

La dimostrazione nel caso dei sottogruppi è del tutto analoga, o addirittura la stessa, tenendo presente che ogni sottogruppo si può scrivere come il ``primo'' di qualcosa.

Un gruppo di Galois grande è una buona cosa

L'ultima affermazione si può invertire.

Proposizione 1   Sia $ E / F$ un'estensione di grado finito.

Supponiamo che l'ordine di $ G = \Gal ( E / F )$ eguagli il grado $ \lvert E : F \rvert $. Allora $ E / F$ è normale.

Dimostrazione. Abbiamo già visto che qualunque sia l'estensione $ E / F$, e posto come al solito $ G = \Gal ( E / F )$, si ha che l'estensione $ E / G'$ è normale, e $ \Gal (E/G') = \Gal (E/F)$. Pertanto

$\displaystyle \lvert E : G' \rvert = \left\lvert G \right\rvert = \lvert E : F \rvert ,$    

e dunque $ \lvert G' : F \rvert = 1$, ovvero $ G' = F$, e $ E / F$ è normale.

Abbiamo visto nel capitolo precedente se $ E / F$ è il campo di spezzamento di un polinomio i cui fattori irriducibili hanno radici distinte, allora

$\displaystyle \left\lvert \Gal ( E / F ) \right\rvert \ge \lvert E : F \rvert .$    

Dato che in generale

$\displaystyle \left\lvert \Gal ( E / F ) \right\rvert \le \lvert E : F \rvert .$    

otteniamo che i due numeri sono eguali, e dunque l'estensione è normale. Abbiamo ottenuto quella che in realtà vedremo essere la caratterizzazione delle estensioni normali di grado finito.

Esercizio 8   Si consideri l'estensione $ \mathbf{Q}(x) / \mathbf{Q}$, ove $ \mathbf{Q}(x)$ è il campo delle funzioni razionali. Si mostri che il sottocampo $ \mathbf{Q}(x^{2})$ è chiuso, mentre non lo è $ \mathbf{Q}(x^{3})$.

next up previous contents
Next: Estensioni normali e campi Up: Le lezioni Previous: Campo di spezzamento   Indice
A. Caranti
2000-05-31