next up previous contents
Next: Corrispondenza di Galois Up: Le lezioni Previous: Richiami   Indice

Subsections

Campo di spezzamento

Se $ F$ è un campo, e $ f \in F[x]$ è monico, di grado positivo, allora una estensione $ E$ di $ F$ si dice campo di spezzamento di $ f$ su $ F$ se valgono

  1. Esistono $ \alpha_{1}, \alpha_{2}, \dots, \alpha_{n} \in E$ tali che

    $\displaystyle f (x) = (x - \alpha_{1}) \cdot ( x - \alpha_{2} ) \cdot \dots ( x - \alpha_{n}).$    

  2. Si ha

    $\displaystyle E = F ( \alpha_{1}, \alpha_{2}, \dots, \alpha_{n} ).$    

La prima condizione dice che in $ E$ ci sono tutte le radici di $ F$. La seconda ha, come vedremo, lo scopo di assicurare l'unicità. Infatti se un campo contiene tutte le radici di un polinomio, anche ogni campo più grande le contiene. Per individuarne uno, la cosa sensata è pertanto prendere il minimo.

Definizione 1   Nella definizione di campo di spezzamento, si intende

$\displaystyle E = F ( \alpha_{1}, \alpha_{2}, \dots, \alpha_{n} ) = F ( \alpha_{1}) ( \alpha_{2}) \dots (\alpha_{n} ),$    

Esercizio 4   Si mostri che

$\displaystyle E = F ( \alpha_{1}, \alpha_{2}, \dots, \alpha_{n} ) = F ( \alpha_{1 \pi}, \alpha_{2 \pi}, \dots, \alpha_{n \pi} )$    

per ogni permutazione $ \pi \in S_{n}$.

Si mostri che se gli $ \alpha_{i}$ sono algebrici su $ F$, allora ogni elemento di $ E$ si scrive come un polinomio negli $ \alpha_{i}$ a coefficienti in $ F$.

Esistenza

Cominciamo col mostrare l'esistenza del campo di spezzamento. Tutto si basa sul seguente

Lemma 1   Sia $ F$ un campo e $ f$ un polinomio monico non costante in $ F[x]$. Allora esistono un anello commutativo $ B$ contenente $ F$, e un elemento $ \alpha \in B$ tali che $ f$ è il polinomio minimo di $ \alpha$ su $ F$.

Una volta trovato un $ B$, non si perde niente a ridefinirlo come

$\displaystyle B = F [ \alpha ] \cong F [ x ] / (f).$    

Con questa ridefinizione, si ha che $ B$ è un campo quando $ f$ è irriducibile su $ F$, altrimenti non è neanche un dominio.

Dimostrazione. Cominciamo col supporre che una simile estensione esista, e consideriamo $ V = F[ \alpha ] \subseteq F$. Abbiamo visto che $ V$ è uno spazio vettoriale su $ F$ di dimensione $ n$, ove $ n$ è il grado di $ f$. Una base di $ V$ su $ F$ è data da

$\displaystyle 1, \alpha, \alpha^{2}, \dots, \alpha^{n-1}.$ (2.1.1)

La mappa

$\displaystyle V$ $\displaystyle \to V$    
$\displaystyle v$ $\displaystyle \mapsto v \cdot \alpha$    

è una mappa lineare. La sua matrice rispetto alla base (2.1.1) è (i miei vettori sono vettori riga)

$\displaystyle A = \begin{bmatrix}0 & 1 & 0 & \dots & 0\\ 0 & 0 & 1 & \dots & 0\... ...& 0 & 0 & \dots & 1\\ -a_{0} & -a_{1} & -a_{2}& \dots & -a_{n-1} \end{bmatrix},$ (2.1.2)

ove $ f = x^{n} + a_{n-1} x^{n-1} + \dots + a_{1} x + a_{0}$. Infatti l'ultima riga di (2.1.2) corrisponde a

$\displaystyle \alpha^{n - 1} \cdot \alpha = \alpha^{n-1} = -a_{0} -a_{1} \alpha -a_{2} \alpha^{2} - \dots -a_{n-1} \alpha^{n-1}.$    

Ora notiamo che si può definire una mappa

$\displaystyle F [\alpha]$ $\displaystyle \to \End_{F} ( F[\alpha] )$    
$\displaystyle \beta$ $\displaystyle \mapsto ( v \mapsto v \cdot \beta ),$    

e che questa mappa è un morfismo iniettivo, che manda $ \alpha$ in $ A$. Ne segue che $ F[\alpha] \cong F[A]$.

A questo punto rivoltiamo la faccenda per costruire l'estensione $ E$ cercata. Consideriamo uno spazio vettoriale $ V$ di dimensione $ n$ su $ F$, e fissiamone una base $ v_{0}, v_{1}, \dots, v_{n-1}$. Sia $ A$ la matrice di (2.1.2). Affermo che $ A$ è l'elemento $ \alpha$ cercato. Cominciamo a osservare che (2.1.2) significa

\begin{displaymath}\begin{gathered}v_{0} A = v_{1}, v_{1} A = v_{2}, \dots, v_{n... ...1} v_{1} - a_{2} v_{2} - \dots - a_{n-1} v_{n-1} \end{gathered}\end{displaymath} (2.1.3)

La prima riga di (2.1.3) ci dice che $ V$ è un modulo ciclico rispetto ad $ A$ (per i dettagli si veda [Jac85]), cioè che partendo dal solo $ v_{0}$ e applicando $ A$ ripetutamente si ottiene un sistema di generatori per $ V$. Sia adesso $ g \in F[x]$. Per verificare che $ g (A) = 0$, cioè che $ g (A)$ sia la mappa nulla su $ V$, sarà sufficiente verificare che valga $ v_{0} g (A) = 0$. Infatti avremo allora

$\displaystyle v_{1} g(A) = v_{0} A g(A) = v_{0} g(A) A = 0,$    
$\displaystyle v_{2} g(A) = v_{1} A g(A) = v_{1} g(A) A = 0,$    
e cosí via,    

dove abbiamo sfruttato il fatto che $ A g(A) = g(A) A$.

Cominciamo allora col vedere che $ v_{0} f(A) = 0$. Infatti, applicando (2.1.3) si ottiene

$\displaystyle v_{0} f(A)$ $\displaystyle = v_{0} (a_{0} + a_{1} A + \dots + a_{n-1} A^{n-1} + A^{n})$    
  $\displaystyle = a_{0} v_{0} + a_{1} v_{1} + \dots + a_{n-1} v_{n-1} +$    
  $\displaystyle \phantom{=\ } -a_{0} v_{0} - a_{1} v_{1} - \dots - a_{n-1} v_{n-1}$    
  $\displaystyle = 0.$    

Invece se $ g(x) = b_{0} + b_{1} x + \dots + b_{n-1} x^{n-1}$ è un polinomio di grado minore di $ n$, grado di $ f$, abbiamo

$\displaystyle v_{0} g(A)$ $\displaystyle = v_{0} (b_{0} + b_{1} A + \dots + b_{n-1} A^{n-1})$    
  $\displaystyle = b_{0} v_{0} + b_{1} v_{1} + \dots + b_{n-1} v_{n-1};$    

dato che i $ v_{i}$ sono una base di $ V$, questo può essere zero solo quando tutti i coefficienti $ b_{i}$ sono zero. Quindi $ f$ ha effettivamente grado minimo fra tutti i polinomi in $ A$ che sia annullano su $ v_{0}$, e quindi su $ V$.

Basta ora prendere $ \alpha = A$ e $ B = F [ A ]$.

Esercizio 5   Sia $ f$ un polinomio monico di grado $ n$ sul campo $ F$. Sia $ E$ un campo di spezzamento di $ f$ su $ F$.

Si mostri che il grado $ \lvert E : F \rvert $ divide $ n !$

(Suggerimento: Procedere per induzione su $ n$, distinguendo il caso $ f$ irriducibile dal caso $ f$ riducibile.)

Una volta in possesso del Lemma 2.1.1, è facile costruire un campo di spezzamento di un polinomio aggiungendo una per una le radici dei suoi fattori irriducibili. Si veda ad esempio [Jac85] per i dettagli.

Unicità

Più sottile è il discorso dell'unicità del campo di spezzamento, che ci porta alla teoria di Galois vera e propria. Il teorema sarebbe questo, ma ci interessano anche i dettagli della dimostrazione

Teorema 1 (Unicità)   Sia $ F$ un campo $ F$, e $ f \in F[x]$ un polinomio monico non costante. Siano $ E_{1}$ e $ E_{2}$ due campi di spezzamento di $ f$ su $ F$. Allora esiste un isomorfismo da $ E_{1}$ a $ E_{2}$ su $ F$.

Con isomorfismo da $ E_{1}$ a $ E_{2}$ su $ F$ si intende un isomorfismo da $ \varphi : E_{1} \to E_{2}$ tale che $ a \varphi = a$ per ogni $ a \in F$. Notate infatti che per definizione $ F$ è contenuto sia in $ E_{1}$ che in $ E_{2}$, e quindi ci può venire il dubbio su cosa succeda ai suoi elementi sotto $ \varphi $.

Notate anche che gli isomorfismi (di anelli) di cui sopra sono anche isomorfismi di spazi vettoriali. C'`e solo da controllare che si tratti di mappe lineari: se $ u, v \in E_{1}$ e $ a, b \in F$, abbiamo

$\displaystyle (a u + b v) \varphi = a \varphi \cdot u \varphi + b \varphi \cdot v \varphi = a (u \varphi ) + b (v \varphi ).$    

Questi isomorfismi sono l'ingrediente base della teoria di Galois, e nel corso della dimostrazione ci interessa anche contarli, cioè vedere quanti sono.

Cominciamo col richiamare un semplice

Lemma 2   Sia $ F$ un campo, $ f \in F[x]$ monico e irriducibile.

Allora gli unici ideali che contengano $ (f)$ sono $ (f)$ stesso e tutto $ F[x]$.

Dimostrazione. $ F[x]$ è un dominio a ideali principali, dunque ogni ideale è della forma $ (g)$, per qualche $ g \in F[x]$. Se $ (g) \supseteq (f)$, si ha $ g \mid f$. Dato che $ f$ è irriducibile, a meno di elementi invertibili si ha o $ g = f$, e dunque $ (g) = (f)$, o $ g = 1$, e dunque $ (g) = F[x]$.

Il primo passo è il seguente Lemma, in cui introduciamo anche uno strumento molto utile.

Lemma 3   Siano $ F$ e $ \overline{F}$ due campi.

Sia $ \bar{\cdot}: F \to \overline{F}$ un isomorfismo. Esso si estende a un ovvio isomorfismo (che continuiamo a chiamare con lo stesso nome) $ \bar{\cdot}:F [x] \to \overline{F}[x]$, quello che manda

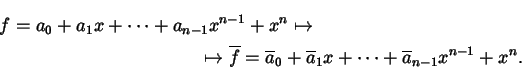
\begin{multline*} f = a_{0} + a_{1} x + \dots + a_{n-1} x^{n-1} + x^{n} \mapst... ...overline{a}_{1} x + \dots + \overline{a}_{n-1} x^{n-1} + x^{n}. \end{multline*}

Sia $ f \in F[x]$ un polinomio monico e irriducibile, e $ \overline{f}\in \overline{F} [x]$ il polinomio corrispondente.

Sia $ K_{1}$ una estensione di $ F$, e $ K_{2}$ una estensione di $ \overline{F}$. Supponiamo ci sia una radice $ \alpha_{1}$ di $ f$ in $ K_{1}$, e una radice $ \alpha_{2}$ di $ \overline{f}$ in $ K_{2}$.

Allora esiste un unico isomorfismo

$\displaystyle \varphi : F[\alpha_{1}] \to \overline{F}[\alpha_{2}]$    

tale che
  1. $ \varphi $ manda $ \alpha_{1}$ in $ \alpha_{2}$
  2. $ \varphi $ ristretto a $ F$ induce $ \bar{\cdot}$

Dimostrazione. L'idea è che abbiamo i morfismi

$\displaystyle \begin{CD}F [\alpha_{1}] @. \overline{F}[\alpha_{2}]\\ @Ag_{1}AA ... ...pi_{f}AA @AA\pi_{\overline{f}}A\\ F[x] @>>\bar{\cdot}> \overline{F}[x] \end{CD}$    

Qui i $ g_{i}$ sono gli isomorfismi dati dai teoremi di struttura delle estensioni semplici $ F [\alpha_{1}]$ e $ \overline{F}[\alpha_{2}]$, e i $ \pi_{i}$ sono gli omomorfismi canonici. Consideriamo il morfismo composto (le mappe le scriviamo a destra, come si è già visto)

$\displaystyle \vartheta = \bar{\cdot}\circ \pi_{\overline{f}} :F[x] \to \overline{F}[x] / (\overline{f})$    

Esso è evidentemente suriettivo, e ha nel nucleo $ f$. Dunque $ \ker(\vartheta )$ è un ideale contenente $ (f)$. Per il Lemma 2.2.2, ci sono due possibilità. Una è $ \ker(\vartheta ) = F[x]$, cioè $ \vartheta $ manda ogni elemento di $ F[x]$ in zero. Ma $ 1 \vartheta = 1 \bar{\cdot}\circ \pi_{\overline{f}} = \overline{1} \pi_{\overline{f}} = \overline{1} + (\overline{f}) \ne 0$, dunque questo è impossibile. Allora vuol dire che $ \ker(\vartheta ) = (f)$: il primo teorema di isomorfismo ci fornisce un isomorfismo

$\displaystyle \eta :\ $ $\displaystyle F[x] / (f) \to \overline{F}[x] / (\overline{f})$    
  $\displaystyle h + (f) \mapsto \overline{h}+ (\overline{f}).$    

Ora abbiamo isomorfismi

$\displaystyle \begin{CD}F [\alpha_{1}] @. \overline{F}[\alpha_{2}]\\ @Ag_{1}AA @AAg_{2}A \\ F[x] / (f) @>>\eta> \overline{F}[x] / (\overline{f})\\ \end{CD}$    

e l'isomorfismo cercato sarà $ g_{1}^{-1} \circ \eta \circ g_{2}$. In altre parole, l'isomorfismo ottenuto agisce come $ \bar{\cdot}$ sugli elementi di $ F$, e manda $ \alpha_{1}$ in $ \alpha_{2}$. (Se serve si possono dare ulteriori dettagli.)

A questo punto possiamo dimostrare l'unicità. Passeremo attraverso un risultato che, a differenza del Teorema 2.2.1, si presta all'induzione.

Proposizione 4   Siano $ F$ e $ \overline{F}$ due campi.

Sia $ \bar{\cdot}: F \to \overline{F}$ un isomorfismo, e indichiamo ancora con $ \bar{\cdot}:F [x] \to \overline{F}[x]$ la sua estensione agli anelli di polinomi.

Sia $ f \in F[x]$ un polinomio monico non costante, e $ \overline{f}\in \overline{F} [x]$ il polinomio corrispondente.

Sia $ E_{1}$ un campo di spezzamento di $ f$ su $ F$, e $ E_{2}$ un campo di spezzamento di $ \overline{f}$ su $ \overline{F}$.

Allora esiste un isomorfismo da $ E_{1}$ a $ E_{2}$ che ristretto a $ F$ induce $ \bar{\cdot}$.

Dimostrazione. La dimostrazione è facile, una volta che si ha il Lemma 2.2.3. Si procede per induzione sul grado $ \lvert E_{1} : F \rvert $. Se questo è $ 1$, ovvero $ f$ ha tutte le sue radici già in $ F$, non c'è niente da dire. Altrimenti $ f$ non ha tutte le sue radici in $ F$, e dunque ha un fattore irriducibile $ g$ di grado $ m > 1$.

Sia $ \alpha_{1}$ una radice di $ g$ in $ E_{1}$, e sia $ \alpha_{2} \in E_{2}$ una qualsiasi radice del polinomio $ \overline{g}$ corrispondente. Per il Lemma 2.2.3, possiamo estendere $ \bar{\cdot}$ a un isomorfismo $ \vartheta : F[\alpha_{1}] \to \overline{F}[\alpha_{2}]$. Ora $ E_{1}$ è ancora un campo di spezzamento di $ f$ su $ F [\alpha_{1}]$, e $ E_{2}$ è un campo di spezzamento di $ \overline{f}$ su $ \overline{F}[\alpha_{2}]$. Dato che $ \lvert F[\alpha_{1}] : F \rvert = \grado (g) = m > 1$, si avrà

$\displaystyle \lvert E_{1} : F[\alpha_{1}] \rvert < \lvert E_{1} : F \rvert ,$    

e possiamo quindi concludere per induzione.

Il Teorema 2.2.1 si ottiene ora ponendo $ F = \overline{F}$, e $ \bar{\cdot}$ eguale alla mappa identica.

Quanti isomorfismi?

E' interessante andare a vedere quanti isomorfismi diversi si possano ottenere attraverso la Proposizione 2.2.4. Quando dobbiamo selezionare $ \alpha_{2}$, possiamo scegliere quasiasi radice del polinomio irriducibile $ \overline{g}\in \overline{F}[x]$, e otterremo un diverso isomorfismo, dato che stiamo scegliendo immagini diverse per il fissato elemento $ \alpha_{1}$. Supponiamo che $ \overline{g}$ abbia $ m = \grado(g) = \grado(\overline{g})$ radici distinte in $ E_{2}$. Allora le scelte possibili sono $ m$. Quindi abbiamo $ m$ scelte, e nel passaggio dall'estensione $ E / F$ all'estensione $ E/F[\alpha_{1}]$ il grado si divide per $ m$.

Se questo avviene per ogni polinomio $ g$ che compare della dimostrazione, otteniamo quindi alla fine tanti isomorfismi quant'è il grado $ \lvert E_{1} : F \rvert $. Una condizione che garantisce che ogno $ g$ abbia radici distinte è naturalmente che $ f$ abbia radici distinte. In realtà basta meno, basta cioè supporre che i fattori irriducibili di $ f$ in $ F[x]$ abbiano radici distinte. (Più avanti diremo che un polinomio con tale proprietà è separabile.) Infatti i polinomi $ g$ sono fattori di $ f$, e sono irriducibili in $ K[x]$, per qualche estensione $ K / F$. Sfruttiamo allora il seguente

Esercizio 6   Sia $ f \in F[x]$. Sia $ K / F$ una estensione, e sia $ g \in K[x]$ un polinomio che divide $ f$, ed è irriducibile in $ K[x]$.

Allora esiste un fattore irriducibile $ h$ di $ f$ in $ F[x]$ tale che $ g$ divide $ h$.

Dimostrazione. [Suggerimento] Si scriva la fattorizzazione $ f = f_{1} \cdot f_{2} \cdot \dots f_{n}$ di $ f$ in fattori irriducibili in $ F[x]$. Ora $ g$ divide $ f$, ed è irriducibile in $ K[x]$. Dunque deve dividere uno dei fattori $ f_{i}$.

Dunque se ogni fattore irriducibile di $ f$ in $ F[x]$ ha radici distinte, lo stesso vale per ogni fattore irriducibile di $ f$ su qualsiasi estensione $ K / F$.

next up previous contents
Next: Corrispondenza di Galois Up: Le lezioni Previous: Richiami   Indice
A. Caranti
2000-05-31