next up previous contents
Next: Chiusure spezzanti e chiusure Up: Le lezioni Previous: Corrispondenza di Galois   Indice

Subsections

Estensioni normali e campi di spezzamento

Un lemma fondamentale

Il seguente risultato comincia a mostrare come una estensione normale algebrica sia legata ai campi di spezzamento.

Teorema 1   Sia $ E / F$ una estensione normale.

Sia $ f \in F[x]$ un polinomio monico e irriducibile.

Se $ f$ ha una radice $ \alpha$ in $ E$, allora $ f$ si spezza in $ E[x]$ nel prodotto di fattori distinti di primo grado.

In particolare, dunque, $ E$ contiene un campo di spezzamento per $ f$, e $ f$ ha tutte le sue radici distinte.

Dimostrazione. Sia $ \Omega = \left\{\, \alpha_{1}, \dots, \alpha_{m} \,\right\}$ (con $ \alpha = \alpha_{1}$) l'insieme delle immagini distinte di $ \alpha$ sotto gli elementi di $ G = \Gal ( E / F )$ radici di $ f$ in $ E$; dunque $ \alpha_{i} \ne \alpha_{j}$ per $ i \ne j$. Consideriamo il polinomio in $ E[x]$

$\displaystyle \tilde{f} = (x - \alpha_{1}) \cdot \dots \cdot (x - \alpha_{m})$ (4.1.1)

Esso divide $ f$, dato che gli $ \alpha_{i}$ sono distinti, e dunque $ \grado(\tilde{f}) = m \le n = \grado (f)$.

Chi sono i coefficienti di $ f$ in termini degli $ \alpha_{i}$? Il coefficiente di $ x^{m}$ è $ 1$. Il coefficiente di $ x^{m-1}$ è

$\displaystyle \alpha_{1} + \alpha_{2} + \dots + \alpha_{m}.$    

Il coefficiente di $ x^{m-2}$ è

$\displaystyle \alpha_{1} \alpha_{2} + \alpha_{1} \alpha_{3} + \dots + \alpha_{n-1} \alpha_{n},$    

ovvero è la somma di tutti i prodotti a due a due degli $ \alpha_{i}$ (distinti). In generale, il coefficiente di $ x^{m-k}$ è

$\displaystyle \sum \left\{\, \alpha_{i_{1}} \cdot \alpha_{i_{2}} \cdot \dots \cdot \alpha_{i_{1}} : 1 \le i_{1} < i_{2} < \dots < i_{k} \le m \,\right\}.$    

Come ulteriore illustrazione, il coefficiente costante è semplicemente il prodotto di tutti gli $ \alpha_{i}$.

Ora tutti questi coefficienti di $ \tilde{f}$ sono funzioni simmetriche negli $ \alpha_{i}$, nel senso che non cambiano se si permutano fra loro gli $ \alpha_{i}$. Dunque essi sono invarianti sotto $ G$, dato che $ G$ non fa altro, appunto, che permutare gli $ \alpha_{i}$. Dato che $ E / F$ è normale, ho che $ G' F$, e dunque i coefficienti di $ \tilde{f}$ sono in $ F$, cioè $ \tilde{f} \in F[x]$.

Ora $ f$ è monico e irriducibile, e $ \tilde{f}$ è un suo divisore monico non costante. Dunque $ f = \tilde{f}$, e abbiamo ottenuto la fattorizzazione`(4.1.1) cercata.

Separabilità

Un polinomio irriducibile $ f \in F[x]$ si dice separabile se ha radici distinte nel suo campo di spezzamento. Ciò equivale a dire che $ (f, f') = 1$. Sia $ E / F$ una estensione algebrica. Un elemento $ a \in E$ si dice separabile su $ F$ se se il suo polinomio minimo su $ F$ è separabile. L'intera estensione è separabile se ogni suo elemento lo è. Contrariamente a quel che scrive Kaplansy, non mi pare inoltre che ci sarebbe niente di male a dire che un polinomio $ f \in F[x]$ è separabile se i suoi fattori irriducibili in $ F[x]$ lo sono.

Abbiamo già visto una parte del seguente

Teorema 1   Sia $ E / F$ un'estensione di grado finito, dunque algebrica. Sono equivalenti
  1. $ E / F$ è normale.
  2. $ E$ è il campo di spezzamento su $ F$ di un polinomio i cui fattori irriducibili sono separabili.
  3. $ E / F$ è separabile, ed $ E$ è un campo di spezzamento su $ F$.

Dimostrazione. Abbiamo già visto nella parte finale del capitolo sui campi di spezzamento che la seconda condizione implica la prima. E' facile vedere che la terza implica la seconda. Resta da vedere che la prima implichi la terza.

Dato che $ E$ ha grado finito su $ F$, si può scrivere $ E = F (\alpha_{1}, \dots, \alpha_{n})$, per esempio prendendo gli $ \alpha_{i}$ come una base di $ E$ su $ F$. Sia $ f_{i}$ il polinomio minimo di $ \alpha_{i}$ su $ F$. Per il Teorema 4.1.1, ogni $ f_{i}$ ha radici distinte, cioè ogni $ f_{i}$ è separabile, e queste radici sono tutte in $ E$. Dunque $ E$ è il campo di spezzamento su $ F$ del polinomio $ f = f_{1} \cdot \dots \cdot f_{n}$, i cui fattori irriducibili $ f_{i}$ sono invero separabili.

Radici multiple

Ricordiamo dal corso di Algebra che vale il seguente

Lemma 1   Sia $ F$ un campo, $ f \in F[x]$. Un elemento $ \alpha$ in una estensione $ E$ di $ F$ è una radice multipla di $ f$ se e solo se $ \alpha$ è radice sia di $ f$ che di $ f'$, e quindi è radice del massimo comun divisore $ (f, f')$.

Ne segue che $ f$ ha radici multiple nel suo campo di spezzamenti se e solo se $ (f, f') \ne 1$.

Sia $ f \in F[x]$ irriducibile. Se $ f' \ne 0$, allora $ \grado (f') < \grado(f)$, dunque anche il grado del massimo comune divisore $ (f, f')$ è minore del grado di $ f$. Dato che $ f$ è irriducibile, ne segue che $ (f, f') = 1$, e dunque $ f$ non ha radici multiple. Pertanto se un polinomio irriducibile ha radici multiple, la sua derivata deve essere zero. Dunque si ha

$\displaystyle f = x^{n} + a_{n-1} x^{n-1} + \dots + a_{1} x + a_{0},$    
$\displaystyle f' = n x^{n-1} + (n-1) a_{n-1} x^{n-2} + \dots + a_{1} = 0,$    
$\displaystyle n = (n-1) a_{n-1} = \dots = i a_{i} = \dots a_{1} = 0.$    

Ora già $ n = 0$ è impossibile in caratteristica zero, mentre se la caratteristica di $ F$ è un primo $ p$ le eguaglianze sono verificate quando $ a_{i} = 0$ se $ p$ non divide $ i$. Dunque $ f$ ha derivata zero se è della forma

$\displaystyle f (x) = x^{p m} + b_{m-1} x^{p (m - 1)} + \dots + b_{1} x^{p} + b_{0},$    

ovvero $ f(x) = g(x^{p})$, ove

$\displaystyle g (x) = x^{m} + b_{m-1} x^{m - 1} + \dots + b_{1} x + b_{0}.$    

Campi finiti

Ricordiamo dal corso di Algebra che un campo finito $ E$ ha ordine $ p^{n}$, ove $ p$ è un primo, contiene il campo $ F$ con $ p$ elementi, ed è il campo di spezzamento su $ F$ del polinomio $ f = x^{p^{n}} - x$. Dai risultati generali sui campi di spezzamento, segue l'unicità, a meno di isomorfismi su $ F$, del campo con $ p^{n}$ elementi.

Ora $ f' = p^{n} x^{p^{n}-1} - 1 = -1$, dunque $ (f, f') = 1$, e $ f$ ha radici distinte. Per il Teorema 4.2.1, $ E / F$ è una estensione normale, di grado $ n$. Il gruppo di Galois $ G = \Gal ( E / F )$ ha dunque ordine $ n$. La regola del binomio in caratteristica $ p$ ci dice che la mappa (morfismo di Frobenius)

$\displaystyle \varphi :\ $ $\displaystyle E \to E$    
  $\displaystyle a \mapsto a^{p}$    

è un automorfismo di $ E$, e fissa gli elementi di $ F$, per il Teorema di Eulero-Fermat. Dunque $ \varphi \in G$. Si vede subito che $ a \varphi ^{i} = a^{p^{i}}$. Dunque se $ 0 < i < n$ gli elementi $ a \in E$ fissati da $ \varphi ^{i}$ sono le radici del polinomio $ x^{p^{i}} - x$. Dato che questo polinomio ha al più $ p^{i} < p^{n}$ radici, $ \varphi ^{i}$ non è la mappa identica su $ E$. Invece $ \varphi ^{n}$ lo è, dato che si vede in Algebra che ogni elemento di $ E$ è radice di $ x^{p^{n}} - x$. Dunque $ \varphi $ ha periodo $ n$, e quindi $ G = \left\langle\, \varphi \,\right\rangle $ è ciclico.

E' ora facile vedere chi sono i campi intermedi fra $ F$ e $ E$. Infatti ricordiamo da Algebra che il gruppo ciclico $ G$ ha uno e un solo sottogruppo di indice $ m$, per ogni divisore $ m$ di $ n$, e questo sottogruppo è $ \left\langle\, \varphi ^{m} \,\right\rangle $. Dunque c'è un sottocampo $ L$ di grado $ \lvert L : F \rvert = m$ per ogni divisore $ m$ di $ n$. Dato che $ \left\lvert L \right\rvert = p^{m}$, si ha che $ L$ deve essere l'unico campo finito con $ p^{m}$ elementi. In effetti per la teoria si ha

$\displaystyle L$ $\displaystyle = \left\langle\, \varphi ^{m} \,\right\rangle '$    
  $\displaystyle = \left\{\, a \in E : a \varphi ^{m} = a \,\right\}$    
  $\displaystyle = \left\{\, a \in E : \text{$a$\ \\lq e radice di $x^{p^{m}} - x$} \,\right\}$    

Esercizio 9   Si provi a dimostrare direttamente questo fatto, che segue dalla teoria appena vista.

Sia $ p$ un primo, $ F$ il campo con $ p$ elementi. Sono equivalenti:

  1. $ x^{p^{m}} - x$ divide $ x^{p^{n}} - x$ in $ F[x]$;
  2. $ p^{m} - 1$ divide $ p^{n} - 1$;
  3. $ m$ divide $ n$

Sia $ F$ il campo con $ p$ elementi, e $ f \in F[x]$ un polinomio irriducibile di grado $ n$. Sia $ E = F(\alpha)$, con $ f(\alpha) = 0$, Dunque $ \lvert E : F \rvert = n$, e $ E$ è il campo con $ p^{n}$ elementi. Dato che $ E / F$ è normale, e $ f$ ha una radice in $ E$, ne segue dal Teorema 4.1.1 che $ f$ ha tutte le sue radici in $ E$, e queste sono distinte. Quindi su un campo finito tutti i polinomi irriducibili sono separabili.

Unicità dei campi finiti

Abbiamo ricordato che un campo finito ha ordine $ p^{n}$, per qualche primo $ p$, e che è campo di spezzamento del polinomio $ x^{p^{n}} - x$. Dal risultato generale per l'unicità di un campo di spezzamento segue anche l'unicità del campo finito di ordine $ p^{n}$.

C'è anche un modo più elementare di vedere questa unicità, che si base sul risultato visto ad Algebra che il gruppo moltiplicativo di un campo finito è ciclico, e dunque il campo è estensione semplice, della forma $ F(\alpha)$.

Sia $ g \in F[x]$ un polinomio monico e irriducibile di grado $ n$, ove $ F = \mathbf{Z}/ p \mathbf{Z}$ è il campo con $ p$ elementi. Sia $ \alpha$ una sua radice in qualche estensione. Dunque $ F(\alpha)$ è un campo con $ p^{n}$ elementi. Ogni elemento di $ F(\alpha)$ è radice di $ x^{p^{n}} - x$. Dunque $ x^{p^{n}} - x$ e $ g$ hanno in comune il fattore $ x - \alpha$. Dato che $ g$ è irriducibile in $ F[x]$, vuole dire che $ g$ divide $ x^{p^{n}} - x$. Abbiamo visto che ogni polinomio irriducibile di grado $ n$ divide $ x^{p^{n}} - x$. Dunque un qualsiasi campo di spezzamento di $ x^{p^{n}} - x$ contiene tutte le radici dei polinomi irriducibili di grado $ n$, e quindi tutti i campi finiti di ordine $ p^{n}$, che abbiamo visto essere della forma $ F(\alpha)$, per queste radici $ \alpha$.

Un campo di spezzamento non normale

Abbiamo visto che per avere un polinomio irriducibile con radici non distinte bisogna essere in caratteristica $ p > 0$. Però i campi finiti, pur avendo caratteristica un primo $ p$, danno estensioni normali. Per vedere un esempio di campo di spezzamento non normale, occorre quindi passare a campi infiniti.

Sia $ K = \GF(p)$ il campo con $ p$ elementi, $ p$ un numero primo. Sia $ E = K(t)$ il campo delle funzioni razionali nell'indeterminata $ t$. Sia $ F = K(t^{p})$. Notiamo che $ t \notin F$. Se infatti

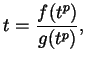$\displaystyle t = \frac{f(t^{p})}{g(t^{p})},$   con $ f, g \in K[t]$, e $ g \ne 0$    

allora $ t g(t^{p}) = f(t^{p})$. Se adesso $ n = \grado(f)$, e $ m = \grado(g)$, otteniamo $ 1 + m p = n p$, un assurdo.

Ora $ E = F(t)$, con $ t$ algebrico su $ F$, dato che $ t$ è radice del polinomio $ \psi (x) = x^{p} - t^{p} \in F[x]$. Dico che $ \psi(x)$ è irriducibile in $ F[x]$. Questo seguirà da un risultato più generale che vedremo più avanti (Lemma 9.1.2); ne diamo qui una semplice dimostrazione ad hoc. Per la nota proprietà del binomio di Newton in caratteristica $ p$ prima abbiamo $ \psi(x) = (x - t)^{p}$ in $ E[x]$. Dunque se $ \psi$ si fattorizza propriamente in $ F[x]$, dovremo avere

$\displaystyle \psi (x) = (x - t)^{\alpha} \cdot (x - t)^{\beta},$    

con $ 0 < \alpha, \beta < p$, e $ (x - t)^{\alpha}, (x - t)^{\beta} \in F[x]$. Ma allora $ (x - t)^{\alpha} = x^{\alpha} - \alpha t x^{\alpha-1} + \dots \in F[x]$, e dunque $ \alpha t \in F$. Ma $ \alpha \ne 0$ in $ K$, e dunque $ t \in F$, una contraddizione.

Dato che $ \psi$ è irriducibile in $ F[x]$, ne segue che $ \psi$ è il polinomio minimo di $ t$ su $ F$. Quindi $ \lvert E : F \rvert = \lvert F(t) : F \rvert = p$. Dato che $ \psi(x) = (x - t)^{p}$, si ha che $ t$ è l'unica radice di $ \psi$ in $ E$, con molteplicità $ p$. Dato che un elemento di $ G = \Gal ( E / F )$ deve mandare $ t$ in un'altra radice del suo polinomio minimo, abbiamo $ G = \{ 1 \}$.

$ E / F$ è quindi un esempio di campo di spezzamento non normale, dato che $ \lvert E : F \rvert = p$, e $ \left\lvert G \right\rvert = 1$. La ragione, come abbiamo visto, è che il polinomio irriducibile $ \psi$ non ha radici distinte.

next up previous contents
Next: Chiusure spezzanti e chiusure Up: Le lezioni Previous: Corrispondenza di Galois   Indice
A. Caranti
2000-05-31