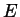 è un campo di spezzamento su
è un campo di spezzamento su 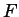
- Se un polinomio monico e irriducibile
![$ f \in F[x]$](img53.gif) ha una
radice in
ha una
radice in 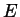 , allora le ha tutte.
, allora le ha tutte.
Notiamo intanto il seguente utile Lemma, che caratterizza i campi di spezzamento senza che si debba nominare esplicitamente un polinomio.
Supponiamo adesso che ![]() sia il campo di spezzamento su
sia il campo di spezzamento su ![]() di un
polinomio
di un
polinomio
![]() . Sia per assurdo
. Sia per assurdo
![]() un polinomio
monico e irriducibile che abbia una radice
un polinomio
monico e irriducibile che abbia una radice
![]() , ma una
radice
, ma una
radice
![]() . Consideriamo i campi
. Consideriamo i campi
![]() ,
, ![]() , ed
, ed
![]() . Come al solito, c'è un
isomorfismo su
. Come al solito, c'è un
isomorfismo su ![]() fra
fra ![]() e
e ![]() , dato che
, dato che ![]() e
e
![]() sono radici dello stesso polinomio irriducibile
sono radici dello stesso polinomio irriducibile ![]() . Inoltre
. Inoltre
![]() è ancora il campo di spezzamento su
è ancora il campo di spezzamento su ![]() di
di ![]() , e
, e
![]() è il campo di spezzamento su
è il campo di spezzamento su ![]() di
di ![]() . Per il
Teorema di unicità 2.2.1, l'isomorfismo su
. Per il
Teorema di unicità 2.2.1, l'isomorfismo su ![]() fra
fra
![]() ed
ed ![]() si estende a un isomorfismo fra
si estende a un isomorfismo fra
![]() e
e ![]() . Ma questo è un isomorfismo su
. Ma questo è un isomorfismo su ![]() , e
quindi dovrebbe in particolare essere un isomorfismo di spazi
vettoriali su
, e
quindi dovrebbe in particolare essere un isomorfismo di spazi
vettoriali su ![]() , e quindi conservare le dimensioni, dunque i
gradi. Ma
, e quindi conservare le dimensioni, dunque i
gradi. Ma
Come accennato, molta della teoria finora trattata si può estendere a estensioni algebriche, di grado anche infinito. Per esempio per il risultato appena visto occorre sostituire l'argomento sulle dimensioni, che perde significato, con il seguente, che comunque si dimostra riducendosi al caso di grado finito.
Allora ![]() è suriettivo.
è suriettivo.
In realtà dato che nei campi gli unici ideali sono lo zero e tutto,
la condizione che il morfismo sia iniettivo è superflua, dato che
chiediamo già che sia l'identità su ![]() , e quindi non sia nullo.
, e quindi non sia nullo.
Supponiamo ora di avere una estensione di grado finito ![]() , e di
voler ampliare
, e di
voler ampliare ![]() a un campo di spezzamento su
a un campo di spezzamento su ![]() . Il risultato
appena visto non ci lascia scelta. Scriviamo
. Il risultato
appena visto non ci lascia scelta. Scriviamo
![]() , e sia
, e sia ![]() il polinomio minimo di
il polinomio minimo di
![]() su
su
![]() . Allora un campo di spezzamento che contenga
. Allora un campo di spezzamento che contenga ![]() deve contenere
tute le radici degli
deve contenere
tute le radici degli ![]() , per il risultato appena visto. Dunque il
più piccolo campo di spezzamento che contenga
, per il risultato appena visto. Dunque il
più piccolo campo di spezzamento che contenga ![]() deve essere il
campo di spezzamento
deve essere il
campo di spezzamento ![]() su
su ![]() si
si
![]() . Se
. Se
![]() è separabile, allora il polinomio
è separabile, allora il polinomio ![]() è separabile, e
otteniamo che
è separabile, e
otteniamo che ![]() è normale.
è normale.
![]() si dice la chiusura spezzante di
si dice la chiusura spezzante di ![]() . Qualora
. Qualora ![]() sia
separabile,
sia
separabile, ![]() si dice chiusura normale di
si dice chiusura normale di ![]() .
.
E' utile per il seguito vedere come ![]() si possa costruire a partire
da
si possa costruire a partire
da ![]() . Cercando di evitare notazioni troppo pesanti,
. Cercando di evitare notazioni troppo pesanti, ![]() è
generata su
è
generata su ![]() da tutte le radici dei vari polinomi
da tutte le radici dei vari polinomi ![]() . Sia
. Sia
![]() una di queste radici. Per argomenti familiari, c'è un
isomorfismo su
una di queste radici. Per argomenti familiari, c'è un
isomorfismo su ![]() fra
fra
![]() e
e ![]() che manda
che manda
![]() in
in ![]() . Dato che
. Dato che ![]() è
un campo di spezzamento, in particolare sia su
è
un campo di spezzamento, in particolare sia su
![]() che su
che su
![]() , questo isomorfismo si estende a un elemento
, questo isomorfismo si estende a un elemento
![]() . Dunque
. Dunque
![]() . Ne segue che
. Ne segue che
![]() è generati da tutti i sottocampi
è generati da tutti i sottocampi ![]() , al variare di
, al variare di
![]() , cioè che
, cioè che ![]() è il più piccolo campo che li contiene
tutti. (Si usa dire che è
è il più piccolo campo che li contiene
tutti. (Si usa dire che è ![]() è il compositum, o composto,
degli
è il compositum, o composto,
degli ![]() .)
.)