next up previous contents
Next: L'equazione di terzo grado Up: Le lezioni Previous: Estensioni normali e sottogruppi   Indice

Subsections

Equazioni risolubili per radicali

Caratteristica zero

In questo capitolo supporremo (quando non affermato esplicitamente il contrario) che la caratteristica sia zero. Dunque tutte le estensioni sono separabili, e normale equivale a campo di spezzamento. Si può fare di meglio, vedi ad esempio [Kap95] o [vdW71,vdW91].

Vogliamo caratterizzare quelle equazioni

$\displaystyle x^{n} + a_{n-1} x^{n-1} + \dots + a_{1} x + a_{0} = 0$ (7.1.1)

le cui soluzioni si possano ottenere a partire dai coefficienti $ a_{i}$ mediante formule in cui compaiano le quattro operazioni (cioè somma, prodotto, sottrazione e divisione un elemento $ \ne 0$, che si possono fare in un campo), più estrazioni di radice.

L'equazione di secondo grado

Per esempio sappiamo che l'equazione di secondo grado $ x^{2} + a_{1} x + a_{0} = 0$ ha soluzioni

$\displaystyle x = \frac{- a_{1} \pm \sqrt{a_{1}^{2} - 4 a_{0}}} {2},$ (7.2.1)

ove occorre solo notare che la formula non ha senso se la caratteristica è $ 2$. Vale la pena di ricordare la dimostrazione, che si fa ``completando il quadrato''. L'idea è di cercare di completare i termini $ x^{2} + a_{1} x$ al quadrato di qualcosa della forma $ (x + b)^{2} = x^{2} + 2 b x + b^{2}$. Dovremo quindi scegliere $ 2 b = a_{1}$, o $ b = a_{1} / 2$. Dunque

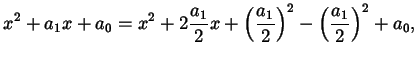$\displaystyle x^{2} + a_{1} x + a_{0} = x^{2} + 2 \frac{a_{1}}{2} x + \left( \frac{a_{1}}{2} \right)^{2} - \left( \frac{a_{1}}{2} \right)^{2} + a_{0},$    

dove abbiamo ``aggiunto e tolto'' il quadrato $ b^{2} = (a_{1}/2)^{2}$. Otteniamo

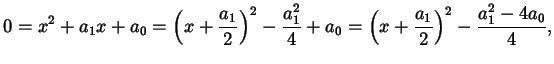$\displaystyle 0 = x^{2} + a_{1} x + a_{0} = \left( x + \frac{a_{1}}{2} \right)^... ...a_{0} = \left( x + \frac{a_{1}}{2} \right)^{2} - \frac{a_{1}^{2} - 4 a_{0}}{4},$    

che ha quindi per soluzione

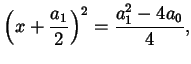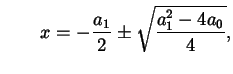$\displaystyle \left( x + \frac{a_{1}}{2} \right)^{2} = \frac{a_{1}^{2} - 4 a_{0}}{4},$   ovvero$\displaystyle \qquad x = - \frac{a_{1}}{2} \pm \sqrt{\frac{a_{1}^{2} - 4 a_{0}}{4}},$    

che si riduce subito a (7.2.1).

Eliminare un coefficiente

In realtà questo ragionamento ha una portata più generale. Supponiamo di voler trovare una formula per le soluzioni dell'equazione (7.1.1) in termini dei coefficienti, sul modello di quella (7.2.1) per l'equazione di secondo grado. Sia $ F$ il campo da cui partiamo, sia $ E / F$ il campo di spezzamento, e siano $ \alpha_{1}, \alpha_{2}, \dots, \alpha_{n} \in E$ le radici. Come abbiamo visto nella dimostrazione del Teorema 4.1.1, abbiamo

$\displaystyle a_{n-1} = \alpha_{1} + \alpha_{2} + \dots + \alpha_{n}.$    

Facciamo la sostituzione

$\displaystyle x = y + \frac{a_{n-1}}{n},$   ovvero$\displaystyle , \qquad y = x + \frac{a_{n-1}}{n},$ (7.3.1)

in (7.1.1). Otteniamo un'equazione

$\displaystyle y^{n} + b_{n-1} y^{n-1} + \dots + b_{1} y + b_{0} = 0,$    

le cui soluzioni sono, tenendo conto di (7.3.1), i numeri

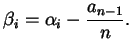$\displaystyle \beta_{i} = \alpha_{i} - \frac{a_{n-1}}{n}.$    

Ne segue che

$\displaystyle b_{n-1}$ $\displaystyle = \beta_{1} + \beta_{2} + \dots + \beta_{n}$    
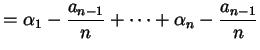  $\displaystyle = \alpha_{1} - \frac{a_{n-1}}{n} + \dots + \alpha_{n} - \frac{a_{n-1}}{n}$    
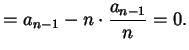  $\displaystyle = a_{n-1} - n \cdot \frac{a_{n-1}}{n} = 0.$    

Dunque con la sostituzione  (7.3.1) si può sempre supporre che in un'equazione di grado $ n$ il coefficiente di $ x^{n-1}$ sia zero.

Estensioni radicali e gruppi risolubili

Appare sensata la seguente definizione. Una estensione $ E / F$ si dice radicale se esistono $ \alpha_{1}, \dots, \alpha_{n} \in E$ tali che $ E = F (\alpha_{1}, \dots, \alpha_{k} )$, ed interi $ n_{i} \ge 1$ tali che per ogni $ i$

$\displaystyle \alpha_{i}^{n_{i}} \in F (\alpha_{1}, \dots, \alpha_{i-1} ).$    

Qui se $ i = 1$ si intende che il termine di destra è semplicemente $ F$. Dunque $ \alpha_{i}$ è algebrico su $ F (\alpha_{1}, \dots, \alpha_{i-1} )$, dato che è radice del polinomio

$\displaystyle f_{i} (x) = x^{n_{i}} - \alpha_{i}^{n_{i}} \in F (\alpha_{1}, \dots, \alpha_{i-1} ) [x].$    

Quindi l'estensione $ E / F$ è di grado finito.

Vale la pena notare che inserendo ulteriori elementi si può sempre supporre che gli $ n_{i}$ siano numeri primi. Ad esempio, se ho che $ \alpha_{1}^{6} \in F$, posso inserire $ \beta = \alpha_{1}^{2}$, in modo che $ \alpha_{1}^{2} \in F (\beta)$, e $ \beta^{3} = \alpha_{1}^{6} \in F$.

Come è fatto il gruppo di Galois di una estensione radicale e normale? (Vedremo tra poco perché quest'ultima affermazione non è restrittiva.) Supponiamo per ora per semplicità che tutte le radici $ (n_{1} \cdot n_{2} \cdot \dots n_{k})$-sime dell'unità siano in $ F$. Ora le radici del polinomio $ f_{1} (x)$ sono $ \alpha_{1} \omega$, al variare di $ \omega$ nell'insieme delle radici $ n_{1}$-sime dell'unità. Tute queste radici sono quindi in $ F (\alpha_{1})$. Ne segue che $ F (\alpha_{1})$ è il campo di spezzamento su $ F$ del polinomio $ f_{1}$. Come è fatto il gruppo di Galois $ \Gal (F(\alpha_{1}) / F)$?

Lemma 1   Sia $ L = F(\alpha)$ un'estensione di $ F$, con $ \alpha^{n} \in F$.

Supponiamo che $ F$ contenga le radici $ n$-sime dell'unità.

Allora $ \Gal ( L/F)$ è abeliano.

Dimostrazione. Come sopra $ \alpha$ è radice di $ x^{n} - \alpha^{n} \in F[x]$, e le radici di questo polinomio sono della forma $ \alpha \omega$, con $ \omega \in F$ una radice $ n$-sima dell'unità. Un elemento $ g \in G = \Gal(L/F)$ è completamente determinato da $ \alpha g$, che per le solite ragioni è della forma $ \alpha \omega$, e quindi è determinato da $ \omega$. Siano $ g_{1}, g_{2} \in G$, con $ \alpha g_{i} = \alpha \omega_{i}$. Abbiamo

$\displaystyle \alpha (g_{1} g_{2}) = (\alpha g_{1}) g_{2} = (\alpha \omega_{1})... ...a_{2} \omega_{1} = \alpha \omega_{1} \omega_{2} = \dots = \alpha (g_{2} g_{1}),$    

e quindi $ g_{1} g_{2} = g_{2} g_{1}$, e $ G$ è abeliano.

Tornando alla nostra discussione, abbiamo scoperto che $ \Gal (F(\alpha_{1}) / F)$ è abeliano. D'altra parte $ F(\alpha_{1}) / F$ è normale, dunque $ F(\alpha_{1})' = \Gal ( E / F(\alpha_{1}))$ è un sottogruppo normale di $ \Gal(E/F)$, e

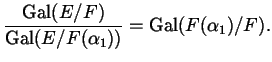$\displaystyle \frac{\Gal ( E / F )}{\Gal ( E / F(\alpha_{1}))} = \Gal (F(\alpha_{1}) / F).$    

Quindi $ G = \Gal ( E / F )$ ha un sottogruppo normale $ N = \Gal ( E / F(\alpha_{1}))$ tale che il quoziente $ G / N$ è abeliano. ora l'estensione $ E / F(\alpha_{1})$ è ancora radicale, per cui $ N = \Gal ( E / F(\alpha_{1}))$ gode della stessa proprietà. Abbiamo ottenuto il seguente risultato provvisorio.

Lemma 2   Sia $ E / F$ un'estensione normale e radicale. Supponiamo che $ F$ contenga le radici dell'unità necessarie, come descritto sopra, e sia $ G = \Gal ( E / F )$.

Allora esistono sottogruppi $ G = N_{0} \ge N_{1} \ge N_{2} \ge \dots \ge N_{k-1} \ge N_{k} = \{ 1 \}$ tali che ogni $ N_{i+1}$ è normale in $ N_{i}$, e il quoziente $ N_{i} / N_{i+1}$ è abeliano.

Dato il contesto, un gruppo con questa proprietà si dice risolubile.

Occorre sottolineare il fatto che se $ M / F$ è una estensione radicale, allora la sua chiusura normale $ L / F$ è ancora una estensione radicale. (Ricordiamo che siamo in caratteristica zero, e dunque ogni estensione è automaticamente separabile). Questo segue dall'argomento in coda al Capitolo 5 - dovrei espanderlo un tantino.

Dato un polinomio monico non costante $ f \in F[x]$, l'equazione corrispondente è $ f(x) = 0$. Sia $ E / F$ un campo di spezzamento di $ f$ su $ F$. Il gruppo di Galois di $ f$ su $ F$ (o dell'equazione corrispondente) è $ \Gal(E/F)$. L'equazione si dice risolubile per radicali se $ E \subseteq M$, ove $ M / F$ è una estensione radicale. Vale allora

Teorema 3   Sia $ f \in F[x]$ monico non costante, $ E / F$ il suo campo di spezzamento. Se $ f = 0$ è risolubile per radicali, allora $ \Gal(E/F)$ è risolubile.

Occorre prima notare il seguente Lemma, senza dimostrazione

Lemma 4 (Proprietà dei gruppi risolubili)  
  1. Se un gruppo è risolubile, allora lo sono anche i suoi sottogruppi e i suoi gruppi quoziente.
  2. Se un gruppo $ G$ ha un sottogruppo normale $ N$ tale che $ N$ e $ G / N$ sono risolubili, allora $ G$ è risolubile.

Cominciamo per il momento a continuare a supporre che $ F$ contenga le radici dell'unità che ci servono per poter applicare il Lemma 7.4.1.

Allora, per dimostrare il Teorema 7.4.3 basta passare da $ M$ alla sua chiusura normale $ N$ su $ F$. Ora $ E / F$ è normale, come campo di spezzamento (in caratteristica zero), dunque $ E$ è stabile rispetto a $ N/F$, e il gruppo $ \Gal(E/F)$ è un quoziente di $ \Gal(N/F)$. Quest'ultimo è risolubile, e quindi lo è anche il primo, per il Lemma appena visto.

E se non ci sono le radici dell'unità?

Se invece in $ F$ non ci sono le radici dell'unità, per poter dimostrare il Teorema 7.4.3 occorre appena un po' più lavoro. Intanto l'argomento appena visto ci riduce a dimostrare che il gruppo di Galois di una estensione radicale e normale $ N/F$ sia risolubile. Sia

$\displaystyle N = F (\alpha_{1}, \dots, \alpha_{k}),$    

con $ \alpha_{i}^{p_{i}} \in F (\alpha_{1}, \dots, \alpha_{i-1})$, per opportuni primi $ p_{i}$, e supponiamo che $ k$ sia il numero più piccolo per cui possiamo fare una cosa del genere. Procederemo per induzione su $ k$.

Consideriamo una radice $ p_{1}$-sima primitiva $ \omega$ dell'unità. Scriviamo $ p = p_{1}$, e $ \alpha = \alpha_{1}$. Consideriamo i campi della Figura 1.

Figura 1: Aggiungere le radici
\begin{figure} \begin{picture}(200,250)(-60,-10) \par\put(-20,-10){$F$} \par\pu... ...-50,200){\circle*{5}} \put(-50,200){\line(1,-4){50}} \end{picture} \end{figure}

Se facciamo vedere che $ \Gal(N(\omega)/F)$ è risolubile, lo sarà anche $ \Gal(N/F)$, che ne è immagine omomorfa.

Ora l'estensione $ F(\omega)/F$ è normale. Se facciamo vedere che il suo gruppo di Galois è abeliano, allora basta vedere che $ \Gal(N(\omega)/F(\omega)$ è risolubile, perché allora lo sarà anche $ \Gal(N(\omega)/F)$, per il Lemma 7.4.4, dato che

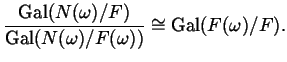$\displaystyle \frac{\Gal(N(\omega)/F)}{\Gal(N(\omega)/F(\omega))} \cong \Gal(F(\omega)/F).$    

Serve il

Lemma 1   Sia $ \omega$ è un radice primitiva $ n$-sima dell'unità su $ F$.

Allora $ \Gal(F(\omega)/F)$ è abeliano.

Dimostrazione. Un elemento $ g \in \Gal(F(\omega)/F)$ manda $ \omega$ in un'altra radice $ n$-sima del'unità, dunque in un $ \omega^{i}$. Un altro $ h \in \in \Gal(F(\omega)/F)$ manda $ \omega$ in $ \omega^{j}$. Dunque

$\displaystyle \omega g h = (\omega^{i}) h = (\omega h)^{i} = \omega^{j i},$    

e naturalmente $ \omega h g = \omega^{i j} = \omega g h$, per cui $ g h = h g$.

Finalmente dobbiamo mostrare che $ \Gal(N(\omega)/F(\omega))$ è risolubile. Notiamo che $ F(\omega, \alpha) / F (\omega)$ è una estensione normale, come campo di spezzamento di $ x^{n} - \alpha^{n}$, che ha lí tutte le sue radici $ \alpha \omega^{i}$. Ma ora $ \Gal(F(\omega, \alpha) / F (\omega))$ è abeliano per 7.4.1. Quindi il problema è spostato sul'estensione normale e radicale $ N(\omega)/F(\omega, \alpha)$, ma dato che

$\displaystyle N(\omega) = F(\omega, \alpha) (\alpha_{2}, \dots, \alpha_{k}),$    

questa adesso ha $ k - 1$ al posto di $ k$, e quindi per l'induzione su $ k$ che avevamo preso all'inizio ha gruppo di Galois risolubile.

Un'equazione non risolubile per radicali

Possiamo ora esibire una equazione non risolubile per radicali.

Notiamo innanzitutto una cosa importante, che per la verità avevamo sostanzialmente già visto nel Capitolo sulla Corrispondenza di Galois. Sia $ f \in F[x]$ un polinomio monico di grado $ n > 0$. Sia $ E / F$ il campo di spezzamento, e $ \alpha_{1}, \dots, \alpha_{n} \in E$ le radici di $ f$. Allora, per argomenti già visti, gli elementi di $ G = \Gal ( E / F )$ mandano ogni $ \alpha_{i}$ in un $ \alpha_{j}$. Dunque $ G$ agisce sull'insieme $ \Omega = \{ \alpha_{1}, \dots, \alpha_{n} \}$. Dato che $ E = F (\alpha_{1}, \dots, \alpha_{n})$, l'azione di $ G$ su $ E$ è determinata dall'azione di $ G$ su $ \Omega$. Cioè la restrizione

$\displaystyle G \to S_{\Omega} \cong S_{n}$    

è iniettiva. Ne segue che $ G$ è (isomorfo a) un sottogruppo di $ S_{n}$.

Consideriamo ora il polinomio

$\displaystyle f(x) = x^{5} - 6 x + 3 \in \mathbf{Q}[x],$    

e sia $ E/\mathbf{Q}$ il suo campo di spezzamento. Si vede subito, con un buon vecchio studio di funzioni, che $ f$ ha tre radici reali e due complesse, dunque coniugate fra loro. Ne segue che il coniugio sui complessi induce un $ 2$-ciclo sull'insieme $ \Omega$ delle radici di $ f$. Il criterio di Eisenstein ci dice subito che $ f$ è irriducibile su $ F$, dunque $ 5$ divide $ \lvert E : \mathbf{Q} \rvert = \left\lvert \Gal(E/\mathbf{Q}) \right\rvert $. Ora si ha il

Lemma 1 (comunemente detto di Cauchy)   Se un gruppo finito ha ordine divisibile per un primo $ p$, allora contiene un elemento di ordine $ p$.

Dimostrazione. Sia $ G$ il gruppo in questione. Consideriamo l'insieme

$\displaystyle B = A^{p} = \left\{\, (a_{0}, a_{1}, \dots, a_{p-1}) : a_{i} \in G \,\right\}.$    

Sia $ S_{p}$ il gruppo delle permutazioni sull'insieme $ \left\{\, 0, 1, \dots, p-1 \,\right\}$. Allora $ S_{p}$ agisce su $ B$ permutando gli indici. Consideriamo il $ p$-ciclo $ \sigma = (0,1,2,\dots,p-1)$, e il sottogruppo $ H = \left\langle\, \sigma \,\right\rangle $ di $ S_{p}$ di ordine $ p$ da lui generato. Anche $ H$ dunque agisce su $ B$.

Consideriamo ora il sottoinsieme di $ B$ dato da

$\displaystyle A = \left\{\, (a_{0}, a_{1}, \dots, a_{p-1}) : a_{i} \in G, a_{0} \cdot a_{1} \cdot \dots \cdot a_{p-1} = 1 \,\right\}.$    

Se $ (a_{0}, a_{1}, \dots, a_{p-1}) \in A$ si ha chiaramente $ a_{p-1} = (a_{0} \cdot a_{1} \cdot \dots \cdot a_{p-2})^{-1}$. Viceversa, scelti elementi arbitrari $ a_{0}, a_{1}, \dots, a_{p-2} \in G$, si ha $ (a_{0}, a_{1}, \dots, a_{p-2}, a_{p-1}) \in A$ per $ a_{p-1} = (a_{0} \cdot a_{1} \cdot \dots \cdot a_{p-2})^{-1}$. Ne segue che $ A$ ha $ \left\lvert G \right\rvert ^{p-1}$ elementi, un numero divisibile per $ p$.

Affermiamo che $ H$ continua ad agire su $ A$. E' sufficiente vedere che $ \sigma$ mandi un elemento di $ A$ in un altro elemento di $ A$. Abbiamo

$\displaystyle (a_{0}, a_{1}, \dots, a_{p-1}) \sigma = (a_{1}, a_{2}, \dots, a_{p-1}, a_{0}),$    

e in effetti se $ (a_{0}, a_{1}, \dots, a_{p-1}) \in A$ abbiamo

$\displaystyle a_{1} \cdot a_{2} \cdot \dots \cdot a_{p-1} \cdot a_{0} = a_{0}^{... ...2} \cdot \dots \cdot a_{p-1}) \cdot a_{0} = a_{0}^{-1} \cdot 1 \cdot a_{0} = 1,$    

e quindi anche $ (a_{1}, a_{2}, \dots, a_{p-1}, a_{0}) \in A$.

Il teorema orbita-stabilizzatore ci dice che la lunghezza di ogni orbita di $ H$ su $ A$ divide l'ordine di $ H$. Dato che $ H$ ha ordine $ p$, un'orbita puó essere lunga $ p$ o $ 1$. In quest'ultimo caso si deve avere in particolare

$\displaystyle (a_{0}, a_{1}, \dots, a_{p-1}) = (a_{0}, a_{1}, \dots, a_{p-1}) \sigma = (a_{1}, a_{2}, \dots, a_{p-1}, a_{0}),$    

e quindi $ a_{0} = a_{1} = \dots = a_{p-1} = a$ per un certo $ a$. Dato che $ (a, a, \dots, a) \in A$, dobbiamo avere $ a^{p} = 1$, e quindi o $ a = 1$, o $ a$ ha ordine $ p$.

Sia $ n_{1}$ il numero di orbite lunghe $ 1$, e $ n_{p}$ il numero di orbite lunghe $ p$. Contando gli elementi di $ A$ si ha

$\displaystyle \left\lvert A \right\rvert = n_{1} + p \cdot n_{p}.$    

Abbiamo visto che $ \left\lvert A \right\rvert $ è divisibile per $ p$, e lo stesso vale per $ p \cdot n_{p}$. Dunque anche $ n_{1}$ è divisibile per $ p$. Ora $ n_{1} \ge 1$, dato che $ (1,1,\dots,1) \in A$. Dunque $ n_{1} \ge p$, e ogni elemento $ a \ne 1$ tale che $ (a, a, \dots, a) \in A$ è un elemento di ordine $ p$.

Dunque $ \Gal(E/\mathbf{Q})$ contiene un elemento di ordine $ 2$ e uno di ordine $ 5$. Ma si ha

Lemma 2   Se un sottogruppo di $ S_{p}$, $ p$ un primo, contiene un elemento di ordine $ 2$ e uno di ordine $ p$, allora è tutto $ S_{p}$.

Dimostrazione. Il 2-ciclo possiamo supporre sia $ \tau = (1, 2)$. Il $ p$-ciclo sarà della forma

$\displaystyle \sigma = (1, a_{2}, a_{3}, \dots, a_{p}).$    

Supponiamo sia $ a_{k+1} = 2$. Allora si ha $ \sigma^{k} = (1, 2, \dots )$, e $ \sigma^{k}$ è ancora un $ p$-ciclo. Si può dunque supporre

$\displaystyle \sigma = (1, 2, 3, \dots, p).$    

Ora $ \tau^{\sigma} = (2, 3)$, e continuando si ottengono tutti i $ 2$-cicli $ (i, i+1)$. (Quando si trova $ p+1$ si intende $ 1$.) A questo punto si vede che $ (1, 2)^{(2, 3)} = (1, 3)$, e poi $ (1, 3)^{(3, 4)} = (1, 4)$. Continuando si ottengono tutti i 2-cicli $ (1, i)$, e quindi il generico 2-cociclo $ (i, j) = (1, j)^{(1, i)}$. Poi si sa che ogni permutazione è prodotto di 2-cocicli.

Permutazioni pari e dispari, e gruppo alterno

Abbiamo già ricordato che ogni permutazione di $ S_{n}$ si può scrivere come prodotto di 2-cicli. Una stessa permutazione si può scrivere in più modi diversi come prodotto di 2-cicli, e da un modo all'altro anche il numero dei 2-cicli può cambiare. per esempio $ (2,3) = (1,2) (1,3) (1,2)$. Si potrebbe però vedere che da un modo all'altro non cambia la parità del numero di 2-cicli che compaiono. In altre parole, se una permutazione si può scrivere come prodotto di un numero pari di 2-cicli, allora non si può scrivere come prodotto di un numero dispari di 2-cicli, e viceversa.

Diciamo che una permutazione è pari o dispari a seconda che il numero di 2-cicli che occorrono per scriverla sia pari o dispari. Si vede subito che il prodotto di due permutazioni pari, o di due dispari, è una permutazione pari, mentre il prodotto di una permutazione pari e di una dispari è una permutazione dispari. Dunque le permutazioni pari di $ S_{n}$ formano un sottogruppo, detto gruppo alterno, e denotato con $ A_{n}$. Se poi $ \sigma \in S_{n} \setminus A_{n}$, ovvero $ \sigma$ è una permutazione dispari, allora $ (1,2) \cdot \sigma$ è pari, dunque $ (1,2) \cdot \sigma \in A_{n}$, e $ \sigma \in (1,2) A_{n}$. Ne segue che $ S_{n} \setminus A_{n} = (1,2) A_{n}$. Quindi $ A_{n}$ ha indice 2 in $ S_{n}$, e in particolare è un sottogruppo normale.

Il gruppo simmetrico su cinque elementi non è risolubile

A questo punto resta solo da vedere che $ S_{5}$ non è risolubile. Ne seguirà che l'equazione

$\displaystyle x^{5} - 6 x + 3 = 0$    

non è risolubile per radicali.

Faremo vedere che il gruppo alterno $ A_{5}$ è semplice, cioè non ha altri sottogruppi normali che $ \left\{\, 1 \,\right\}$ e tutto $ A_{5}$. Inoltre $ A_{5}$ non è abeliano, dato che $ (1 2) (4 5) \cdot (1 3) (4 5) = (1 2 3) \ne (1 3 2) = (1 3) (4 5) \cdot (1 2) (4 5)$. Adesso se $ S_{5}$ fosse risolubile, anche $ A_{5}$ dovrebbe esserlo, per il Lemma 7.4.4. Ma allora $ A_{5}$ dovrebbe avere un sottogruppo normale abeliano diverso da $ \left\{\, 1 \,\right\}$, il che non è.

Vediamo adesso che $ A_{5}$ è semplice. Studieremo le sue classi di coniugio, e poi faremo vedere che i soli sottogruppi normali sono $ \left\langle\, 1 \,\right\rangle $ e $ A_{5}$ stesso.

Abbiamo forse già notato il seguente lemma, che descrive il coniugio in $ S_{n}$:

Lemma 1   Sia $ (i_{1} i_{2} \dots i_{k})$ un ciclo in $ S_{n}$, e $ \sigma \in S_{n}$.

Allora

$\displaystyle (i_{1} i_{2} \dots i_{k})^{\sigma} = \sigma^{-1} (i_{1} i_{2} \dots i_{k}) \sigma = (i_{1}^{\sigma} i_{2}^{\sigma} \dots i_{k}^{\sigma}).$    

Dunque due permutazioni in $ S_{n}$ sono coniugate in $ S_{n}$ se e solo se hanno la stessa struttura ciclica: ovvero lo stesso numero di cicli di una data lunghezza $ k$, per ogni $ k$. Ad esempio $ (1 2 3) (4 5)$ e $ (2 5 3) (1 4)$ sono coniugate sotto la permutazione che manda 1 in 2, 2 in 5, 3 in 3, 4 in 1 e 5 in 4, cioè sotto $ \sigma = (1 2 5 4)$.

Dunque è facile vedere le classi di coniugio in $ S_{5}$:

$ x$ Num. con. $ x$ $ \left\lvert C_{S_{5}}(x) \right\rvert $
1 1 120
(1 2) 10 12
(1 2 3) 20 6
(1 2 3 4) 30 4
(1 2 3 4 5) 24 5
(1 2) (3 4) 15 8
(1 2 3) (4 5) 20 6
Qui la prima colonna indica un elemento rappresentativo $ x$ per ogni possibile struttura ciclica. La seconda indica il numero di elementi con quella struttura ciclica, e quindi il numero di elementi della classe di coniugio $ x^{S_{5}}$ di $ x$ in $ S_{5}$. Nella terza colonna c'è l'ordine del centralizzante di $ x$ in $ S_{5}$, che per il teorema orbita stabilizzatore deve soddisfare

$\displaystyle \left\lvert S_{5} \right\rvert = \left\lvert x^{G} \right\rvert \cdot \left\lvert C_{S_{5}}(x) \right\rvert .$    

Il numero di elementi di $ x^{G}$ si calcola come negli esempi che seguono. Per calcolare il numero dei coniugati di $ (1 2)$, cioè dei 2-cicli $ (i j)$, con $ i \ne j$, si nota che ci sono 5 possibilità per $ i$ e 4 per $ j$. Dato che $ (i j) = (j i)$, il totale è $ 5 \cdot 4 / 2 = 10$. Invece coi 3-cicli si calcola $ 5 \cdot 4 \cdot 3 / 3$, dato che $ (i j k) = (j k i) = (k i j)$. Nel caso del prodotto di due 2-cicli disgiunti, si nota che $ (i j) (k l) = (k l) (i j)$, per cui il calcolo è

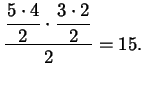$\displaystyle \frac{\displaystyle \frac{5 \cdot 4}{2} \cdot \frac{3 \cdot 2}{2}}{2} = 15.$    

Quando vado a vedere le classi di coniugio di $ A_{5}$, devo incominciare a guardare solo le permutazioni pari, cioè $ 1, (1 2 3), (1 2 3 4 5), (1 2) (3 4)$.

Premettiamo il seguente Lemma

Lemma 2   Sia $ G$ un gruppo finito, $ H, K \le G$. Consideriamo l'insieme $ H K$. Sia ha

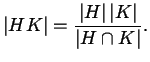$\displaystyle \left\lvert H K \right\rvert = \frac{\left\lvert H \right\rvert \left\lvert K \right\rvert }{\left\lvert H \cap K \right\rvert }.$    

In particolare, se $ H K$ è un sottogruppo, allora

$\displaystyle \lvert H K : K \rvert = \lvert H : H \cap K \rvert .$    

Dimostrazione. L'insieme $ H K$ è unione di classi laterali di $ K$ rispetto a $ H$:

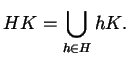$\displaystyle H K = \bigcup_{h \in H} h K.$    

Si tratta di vedere quando sono eguali due classi. Si ha $ h_{1} K = h_{2} K$ se e solo se $ h_{1}^{-1} h_{2} \in K$, e dunque $ h_{1}^{-1} h_{2} \in H \cap K$. Questa è la stessa relazione che da le classi laterali di $ H \cap K$ in $ H$, dunque

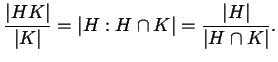$\displaystyle \frac{\left\lvert H K \right\rvert }{\left\lvert K \right\rvert }... ...rvert = \frac{\left\lvert H \right\rvert }{\left\lvert H \cap K \right\rvert }.$    

Ora dimostriamo

Lemma 3   Il gruppo finito $ G$ agisca sull'insieme finito $ \Omega$. Sia $ H$ un sottogruppo di $ G$ di indice 2.

Sia $ \alpha \in \Omega$. Si ha

$\displaystyle \left\lvert \alpha^{H} \right\rvert = \begin{cases}\frac{1}{2} \c... ...le H$,}\\ \left\lvert \alpha^{G} \right\rvert & \text{altrimenti.} \end{cases}$    

Dimostrazione. Abbiamo

$\displaystyle \left\lvert \alpha^{H} \right\rvert$ $\displaystyle = \lvert H : \Stab_{H}(\alpha) \rvert$    
  $\displaystyle = \lvert H : H \cap \Stab_{G}(\alpha) \rvert$    
  $\displaystyle = \frac{\left\lvert H \right\rvert }{\left\lvert H \cap \Stab_{G}(\alpha) \right\rvert }$    
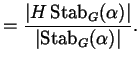
  $\displaystyle = \frac{\left\lvert H \Stab_{G}(\alpha) \right\rvert }{\left\lvert \Stab_{G}(\alpha) \right\rvert }.$    

Ora se $ \Stab_{G}(\alpha) \le H$ questo ordine è

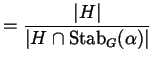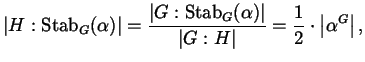$\displaystyle \lvert H : \Stab_{G}(\alpha) \rvert = \frac{\lvert G : \Stab_{G}(... ...\lvert G : H \rvert } = \frac{1}{2} \cdot \left\lvert \alpha^{G} \right\rvert ,$    

mentre se $ \Stab_{G}(\alpha) \not\le H$, allora $ H \Stab_{G}(\alpha) = G$, dato che $ H$ ha indice 2 in $ G$, e quindi $ \left\lvert \alpha^{H} \right\rvert = \lvert G : \Stab_{G}(\alpha) \rvert = \left\lvert \alpha^{G} \right\rvert $.

Dunque le classi di coniugio di elementi $ x$ di $ A_{5}$ sono le stesse che in $ S_{5}$, tranne quando $ C_{S_{5}}(x) \le A_{5}$. Ora sapere l'ordine di questi centralizzanti ci aiuta a sapere chi sono. E in effetti $ (1 2 3)$ è centralizzato dalla permutazione dispari $ (4 5)$, mentre $ (1 2) (3 4)$ è centralizzato dala permutazione dispari $ (1 3 2 4)$ (basta notare che $ (1 3 2 4)^{2} =(1 2) (3 4)$. Invece il centralizzante di $ (1 2 3 4 5)$ ha ordine 5, e dunque

$\displaystyle C_{S_{5}} \left( (1 2 3 4 5) \right) = \left\langle\, (1 2 3 4 5) \,\right\rangle \le A_{5}.$    

Dunque la classe di coniugio di $ (1 2 3 4 5)$ in $ S_{5}$ si spezza in due in $ A_{5}$, e abbiamo la tabella delle classi di coniugio di $ A_{5}$
$ x$ Num. con. $ x$ $ \left\lvert C_{A_{5}}(x) \right\rvert $
1 1 60
(1 2 3) 20 3
(1 2 3 4 5) 12 5
(1 3 5 2 4) 12 5
(1 2) (3 4) 15 4
Si noti che in effetti $ x = (1 2 3 4 5)$ e $ (1 3 5 2 4)$ non sono coniugati in $ A_{5}$, perché sono coniugati sotto la permutazione dispari $ (2 3 5 4)$, e ogni altra permutazione che li coniughi è nella classe laterale $ C_{S_{5}}(x) \cdot(2 3 5 4)$, che è fatta tutta di permutazioni dispari, dato che tutti gli elementi di $ C_{S_{5}}(x)$ sono permutazioni pari.

Adesso se $ N$ è un sottogruppo normale di $ A_{5}$ diverso da $ \left\langle\, 1 \,\right\rangle $, dovrà essere unione disgiunta di alcune delle classi di coniugio, inclusa $ \left\langle\, 1 \,\right\rangle $. Ma si vede facilmente che non si possono raggruppare i numeri di elementi delle classi per formare un divisore di $ 60$ diverso da $ 60$ stesso. Dunque $ A_{5}$ è semplice.

L'equazione generale di $ n$-simo grado

Cominciamo col seguente

Lemma 1   Sia $ E$ un campo. Sia $ G$ un gruppo finito di automorfismi di $ E$. Sia $ F$ il sottocampo di $ E$ degli elementi fissati da $ G$. Allora $ E / F$ è una estensione normale, e $ \Gal(E/F) = G$.

Dimostrazione. Intanto notiamo che $ G$ si può considerare come un sottogruppo di $ \Gal(E/K)$, dove $ K$ è il campo primo.

E' chiaro che $ \Gal(E/F) \ge G$. Per i soliti lemmi, abbiamo $ \left\lvert G \right\rvert \ge \lvert E : F \rvert \ge \left\lvert \Gal(E/F) \right\rvert \ge \left\lvert G \right\rvert $, e dunque si ottiene che tutti i numeri sono eguali. In particolare $ \lvert E : F \rvert = \left\lvert \Gal(E/F) \right\rvert $, e quindi $ E / F$ è normale.

Consideriamo adesso un campo primo $ K$, e il campo $ E = K(t_{1}, t_{2}, \dots, t_{n})$ delle funzioni razionali. Su $ E$ agisce in modo naturale come gruppo di automorfismo il gruppo simmetrico $ G = S_{n}$, permutando gli indici. Il campo $ F$ degli elementi fissati da $ S_{n}$ è detto il campo delle funzioni razionali simmetriche, dato che non cambiano se permuto fra loro le variabili $ t_{1}, t_{2}, \dots, t_{n}$. Si ha quindi $ \lvert E : F \rvert = \left\lvert S_{n} \right\rvert = n!$.

Consideriamo adesso il polinomio

$\displaystyle f(x)$ $\displaystyle = (x - t_{1}) \cdot (x - t_{2}) \cdot \dots (x - t_{n})$    
  $\displaystyle = x^{n} - \sigma_{1} x^{n-1} + \sigma_{2} x^{n-2} + (-1)^{n-1} \sigma_{n-1} + (-1)^{n} \sigma_{n}.$    

Qui $ \sigma_{i}$ è la $ i$-sima funzione simmetrica elementare nei $ t_{1}, t_{2}, \dots, t_{n}$, ovvero la somma di tuti i prodotti di $ i$ elementi distinti fra essi. Ad esempio

$\displaystyle \sigma_{1} = t_{1} + t_{2} + \dots + t_{n}, \qquad \sigma_{n} = t_{1} t_{2} \cdots t_{n}.$    

Dunque $ f(x) \in L[x]$, ove $ L = K(\sigma_{1}, \sigma_{2}, \dots, \sigma_{n}) \subseteq F$, ed $ E$ è il campo di spezzamento di $ f$ su $ L$. Per l'Esercizio 5, si ha $ n! = \lvert E : F \rvert \le \lvert E : L \rvert \le n!$, e dunque $ F = L$. Ne segue l'importante

Teorema 2   Ogni funzione razionale simmetrica è una funzione razionale delle funzioni simmetriche elementari.

Un risultato analogo varrebbe per i polinomi: si veda ad esempio [Jac85].

L'equazione $ f(x) = 0$ viene detta equazione generale di $ n$-simo grado, dato che ogni equazione di $ n$-simo grado si ottiene attribuendo valori particolari ai $ t_{i}$. (Qui ci sarebbe da fare un discorso molto più preciso sul concetto di specializzazione, ma preferisco ometterlo completamente.) Abbiamo visto che il suo gruppo di Galois è $ S_{n}$. Per $ n \ge 5$, abbiamo $ S_{5} \le S_{n}$. Abbiamo visto che $ S_{5}$ non è risolubile, per cui neanche $ S_{n}$ lo è. Ne segue che l'equazione generale di $ n$-simo grado non è risolubile per radicali, per $ n \ge 5$.

Vedremo invece che le equazioni di grado tre e quattro sono risolubili per radicali, dato che $ S_{3}$ e $ S_{4}$ sono gruppi risolubili. Per la verità per ora garantisco solo la dimostrazione per quanto riguarda l'equazione di terzo grado, anche se poi il più è fatto anche per quella di quarto.

Determinante di Vandermonde

La formula seguente è spesso utile

Lemma 1 (Determinante di Vandermonde)  

$\displaystyle \Delta(t_{1}, \dots, t_{n}) = \det \begin{bmatrix}1 & 1 & \dots &... ...ots & t_{n}^{n-1} \\ \end{bmatrix} = \prod_{1 \le i < j \le n} (t_{j} - t_{i}).$ (7.10.1)

Qui i $ t_{i}$ possono essere per esempio indeterminate. L'espressione $ \Delta(t_{1}, \dots, t_{n})$ si dice determinante di Vandermonde.

Dimostrazione. Si può fare una dimostrazione per induzione, i casi $ n = 1, 2$ essendo ovvi. Consideriamo il polinomio

$\displaystyle f(x) = \det \begin{bmatrix}1 & 1 & \dots & 1 & 1\\ t_{1} & t_{2} ... ...\\ t_{1}^{n-1} & t_{2}^{n-1} & \dots & t_{n-1}^{n-1} & x^{n-1} \\ \end{bmatrix}$ (7.10.2)

a coefficienti in $ \mathbf{Z}[t_{1}, t_{2}, \dots, t_{n-1}]$. E' un polinomio di grado $ n-1$, che ha radici distinte $ t_{1}, t_{2}, \dots, t_{n-1}$: infatti sostituendo $ x = t_{i}$, per $ 1 \le i < n$, si ottiene il determinante di una matrice con due colonne eguali, che è zero. Per la regola di Ruffini si ha

$\displaystyle f(x) = C (x - t_{1}) (x - t_{2}) \dots (x - t_{n-1}).$    

Il coefficiente $ C$ si ricava facilmente da (7.10.2), e si vede essere un determinante di Vandermonde su una matrice $ (n-1) \times (n-1)$. Ora $ f(t_{n})$ è proprio il determinante di Vandermonde, per cui si ottiene il risultato.

Da gruppi risolubili a estensioni radicali

Vogliamo ora vedere che se il campo di spezzamento $ E$ su $ F$ di un polinomio $ f(x) \in F[x]$ ha gruppo di Galois risolubile, allora $ E$ è contenuto in una estensione radicale di $ F$.

Anche qui semplificheremo le cose supponendo che $ F$ contenga le radici dell'unità che ci serviranno lungo la strada. Questo farà si' che ci venga fuori addirittura che $ E / F$ è una estensione radicale, cosa che non è vera però quando le radici dell'unità non ci sono.

Se $ G = \Gal ( E / F )$ è risolubile, avrà un sottogruppo normale $ N < G$ tale che il quoziente $ G / N$ sia abeliano. Non sarebbe difficile convincersi che esiste un sottogruppo $ M \le N$ che è ancora normale, ed ha quoziente $ G / M$ di ordine un numero primo $ p$. A questo punto, procedendo per induzione, basta dimostrare il seguente

Lemma 1 (Risolventi di Lagrange)   Sia $ K / F$ una estensione normale tale che il gruppo di Galois $ \Gal(K/F)$ sia ciclico di ordine $ p$ primo.

Supponiamo che $ F$ contenga le radici $ p$-sime dell'unità, e che esse siano distinte. (Quest'ultimo fatto è automatico sotto la nostra condizione generale che la caratteristica sia zero.)

Allora esiste $ \alpha \in K$ tale che $ K = F(\alpha)$ e $ \alpha^{p} \in F$.

Per un tale $ \alpha$ vale $ F(\alpha) \ne F$, e dunque $ F(\alpha) = K$, dato che $ \lvert K : F \rvert = p$, e quindi non ci sono campi intermedi. Dunque $ K / F$ è una estensione radicale.

Applichiamo il Lemma per $ K = M'$. Dato che $ M$ è un sottogruppo normale di $ G = \Gal ( E / F )$, ne segue che $ K / F$ è normale, e $ \Gal(K/F) \cong G / M$ ha ordine $ p$. Dunque da $ F$ a $ K$ si va con una estensione radicale, e poi si va avanti per induzione.

Dimostrazione. Nella dimostrazione si introducono i cosiddetti risolventi di Lagrange, che saranno essenziali anche per trovare le formule risolutive per l'equazione di terzo grado.

Siano $ 1, \omega, \omega^{2}, \dots, \omega^{p-1}$ le radici $ p$-sime dell'unità in $ F$. Sia $ \beta \in K \setminus F$, per cui $ K = F(\beta)$. Sia $ \Gal(K/F) = \left\langle\, g \,\right\rangle $. Dato che l'estensione $ K / F$ è normale, si ha $ \beta g \ne \beta$, e dunque per il teorema orbita-stabilizzatore gli elementi $ \beta, \beta g, \dots, \beta g^{p-1}$ sono distinti.

Consideriamo i risolventi di Lagrange

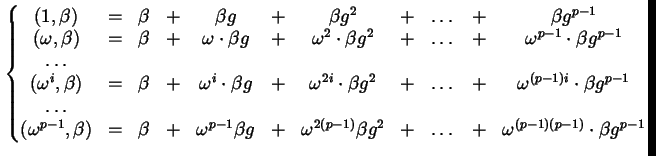$\displaystyle \addtocounter {MaxMatrixCols}{1}\left\{ \begin{matrix}(1, \beta) ... ...^{2} &+& \dots &+& \omega^{(p-1)(p-1)} \cdot \beta g^{p-1} \end{matrix} \right.$    

Abbiamo per ogni $ i$

$\displaystyle (\omega^{i}, \beta) g = \beta g + \omega^{i} \beta g^{2}+ \omega^... ...g^{3} + \dots + \omega^{i (p-1)} \cdot \beta = \omega^{-i} (\omega^{i}, \beta),$    

dato che $ g^{p} = 1$. Dunque

$\displaystyle (\omega^{i}, \beta)^{p} g = \left( (\omega^{i}, \beta) g \right)^... ...= \left( \omega^{-i} (\omega^{i}, \beta) \right)^{p} = (\omega^{i}, \beta)^{p}.$    

Dunque per ogni $ i$ si ha $ (\omega^{i}, \beta)^{p} \in \Gal(K/F)' = F$.

Ora $ (1, \beta), (\omega, \beta) , \dots, (\omega^{p-1}, \beta)$ si esprimono come combinazioni lineari degli $ \beta, \beta g, \dots, \beta g^{p-1}$ mediante una matrice

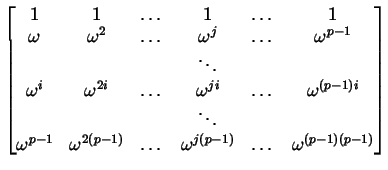$\displaystyle \begin{bmatrix}1 & 1 & \dots & 1 & \dots & 1\\ \omega & \omega^{2... ...(p-1)} & \dots & \omega^{j (p-1)} & \dots & \omega^{(p-1)(p-1)}\\ \end{bmatrix}$    

che ha determinante di Vandermonde $ \Delta(1,\omega, \dots, \omega^{p-1})$. Dato che per ipotesi le $ p$ radici $ p$-sime dell'unità $ 1, \omega, \dots, \omega^{p-1}$ sono distinte, segue dalla formula (7.10.1) che $ \Delta(1,\omega, \dots, \omega^{p-1}) \ne 0$.

Dunque la matrice in questione è invertibile, e si possono scrivere anche i $ \beta, \beta g, \dots, \beta g^{p-1}$ come combinazioni lineari di $ (1, \beta), (\omega, \beta) , \dots, (\omega^{p-1}, \beta)$. Abbiamo naturalmente $ K = F(\beta) = F(\beta, \beta g, \dots , \beta g^{p-1})$. Dunque almeno uno degli $ (\omega^{i}, \beta)$ non sta in $ F$, e si ha quindi $ K = F(\omega^{i}, \beta)$. Il risultato si ottiene ponendo $ \alpha = \omega^{i}, \beta)$.

Un'applicazione banale dei risolventi di Lagrange si ha con l'equazione di secondo grado $ f(x) = x^{2} + a_{1} x + a_{0} = 0$, con $ f \in F[x]$. Sia $ K$ il campo di spezzamento di $ f$ su $ F$. Se supponiamo $ f$ irriducibile in $ F[x]$, allora $ \lvert K : F \rvert = 2$. Stiamo supponendo che la caratteristica sia zero, o almeno diversa da $ 2$, per cui $ f$ è separabile, il gruppo di Galois $ \Gal(K/F)$ è ciclico di ordine $ 2$, e se $ \beta$ è una radice di $ f$, l'altra è $ \beta g$, per $ 1 \ne g \in \Gal(K/F)$. Qui $ \omega = -1$, e abbiamo

\begin{displaymath}\begin{aligned}{}&(1, \beta) = \beta + \beta g = - a_{1} \in F,\\ {}&(-1, \beta) = \beta - \beta g.\\ \end{aligned}\end{displaymath}

Dato che uno di questi due elementi deve stare fuori da $ F$, si ha $ (-1, \beta) \not\in F$, e dunque $ K = F(-1, \beta)$. Inoltre

$\displaystyle (-1, \beta)^{2}$ $\displaystyle = (\beta - \beta g)^{2}$    
  $\displaystyle = \beta^{2} + \left( \beta g \right)^{2} - 2 \beta \cdot \left( \beta g \right)$    
  $\displaystyle = \left( \beta + \beta g \right)^{2} - 4 \beta \cdot \left( \beta g \right)$    
  $\displaystyle = a_{1}^{2} - 4 a_{0}.$    

Dunque $ (-1, \beta) = \sqrt{a_{1}^{2} - 4 a_{0}}$. A questo punto si risolve il sistema (7.11.1) di due equazioni lineari nelle due incognite $ \beta, \beta g$, e si ritrova la solita formula.

E se non ci sono le radici dell'unità?

Rivediamo adesso gli ultimi argomenti senza supporre di avere già a disposizione le radici dell'unità. Vogliamo dimostrare

Teorema 1   Sia $ E / F$ il campo di spezzamento su $ F$ del polinomio monico non costante $ f \in F[x]$. Supponiamo che $ \Gal(E/F)$ sia risolubile.

Allora esiste una estensione radicale $ M / F$ tale che $ M \supseteq E$.

Dimostrazione. Dato che $ G = \Gal ( E / F )$ è risolubile, avrà un sottogruppo normale $ H$ di indice un primo $ p$. Sia $ \omega$ una radice primitiva $ p$-sima dell'unità, e consideriamo i campi della Figura 2.

Figura 2: Aggiungere le radici
\begin{figure} \begin{picture}(200,250)(-60,-10) \par\put(-20,-10){$F$} \par\pu... ...-50,200){\circle*{5}} \put(-50,200){\line(1,-4){50}} \end{picture} \end{figure}

Dato che $ E / F$ è un campo di spezzamento, e la separabilità è sempre garantita dalla caratteristica zero, $ E$ sarà stabile rispetto a $ \Gal(E(\omega)/F)$. In particolare possiamo considerare la restrizione

$\displaystyle \Gal (E(\omega) / F(\omega)) \to \Gal(E / F).$    

Questa restrizione è iniettiva, perché un isomorfismo di $ E(\omega)$ in sé che fissi sia $ \omega$ che gli elementi di $ E$ deve essere l'identità. Dunque $ \Gal (E(\omega) / F(\omega))$ è isomorfo a un sottogruppo di $ \Gal(E/F)$ . Procediamo per induzione sull'ordine del gruppo di Galois. Se $ \Gal (E(\omega) / F(\omega))$ ha ordine più piccolo di quello di $ \Gal(E/F)$, allora per induzione c'è una estensione radicale $ M/F(\omega)$, con $ M \supseteq E(\omega)$. Allora anche $ M / F$ è una estensione radicale, e $ M \supseteq E$, come richiesto.

Se invece gli ordini sono gli stessi, allora $ \Gal (E(\omega) / F(\omega))$ e $ \Gal(E/F)$ sono gruppi isomorfi. Dunque anche $ \Gal (E(\omega) / F(\omega))$ ha un sottogruppo $ K$, normale, di indice $ p$. Consideriamo $ K'$ come in figura. Allora $ \lvert K' : F(\omega) \rvert = p$, e l'estensione $ K' / F(\omega)$ è normale, perché $ K$ è un sottogruppo normale di $ \Gal (E(\omega) / F(\omega))$. A questo punto posso applicare il Lemma 7.11.1, e ottenere che $ K' = F(\omega, \alpha)$, con $ \alpha^{p} \in F(\omega)$. Quindi da $ F$ a $ K'$ siamo andati con una estensione radicale, e ora possiamo applicare l'ipotesi induttiva a $ E(\omega)/K'$.

next up previous contents
Next: L'equazione di terzo grado Up: Le lezioni Previous: Estensioni normali e sottogruppi   Indice
A. Caranti
2000-05-31